题目内容
7.已知{an}中,${a_n}={n^2}+λn$,且{an}是递增数列,则实数的取值范围是( )| A. | (-2,+∞) | B. | [-2,+∞) | C. | (-3,+∞) | D. | [-3,+∞) |
分析 由于{an}是递增数列,可得?n∈N*,an+1>an,即(n+1)2+λ(n+1)>n2+λn,解出利用数列的单调性即可得出.
解答 解:∵{an}是递增数列,
∴?n∈N*,an+1>an,
∴(n+1)2+λ(n+1)>n2+λn,
λ>-(2n+1),
∴λ>-3.
故选:C.
点评 本题考查了数列的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
 ,
, ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 是函数
是函数 的反函数,则
的反函数,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.
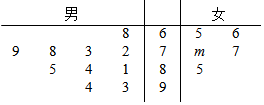 某校组织学生参加数学竞赛,共有15名学生获奖,其中10名男生和5名女生,其成绩如茎叶图所示(单位:分).规定:成绩在80分以上者为一等奖,80分以下者为二等奖,已知这5名女生的平均成绩为73.
某校组织学生参加数学竞赛,共有15名学生获奖,其中10名男生和5名女生,其成绩如茎叶图所示(单位:分).规定:成绩在80分以上者为一等奖,80分以下者为二等奖,已知这5名女生的平均成绩为73.