题目内容
已知函数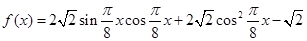 ,
,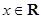 .
.
(1)求函数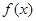 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)若函数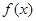 图象上的两点
图象上的两点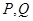 的横坐标依次为
的横坐标依次为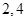 ,
,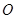 为坐标原点,求
为坐标原点,求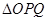 的外接圆的面积.
的外接圆的面积.
(1)最小正周期为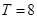 ,单调递增区间是
,单调递增区间是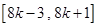 (
(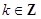 );(2)
);(2)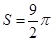 .
.
解析试题分析:(1)首先应用三角函数公式,化简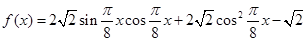 得到
得到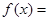
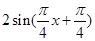 ,其最小正周期为
,其最小正周期为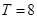 ,由复合函数的单调性,根据
,由复合函数的单调性,根据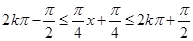 解得函数
解得函数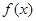 的单调递增区间是
的单调递增区间是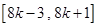 (
(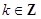 );
);
(2)由已知求得,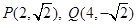 .
.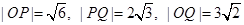
从而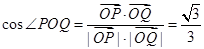 ,
,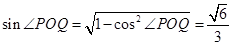 ,
,
由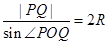 ,求得
,求得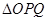 的外接圆的半径为
的外接圆的半径为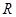 ,进一步计算.
,进一步计算.
试题解析:(1)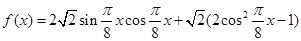
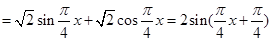 , 2分
, 2分
所以,函数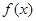 的最小正周期为
的最小正周期为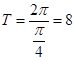 . 3分
. 3分
由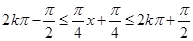 (
(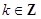 )得
)得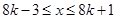 (
(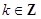 ),
), 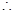 函数
函数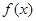 的单调递增区间是
的单调递增区间是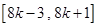 (
(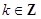 ) 5分
) 5分
(2)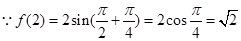 ,
, 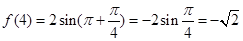 ,
,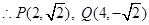 7分
7分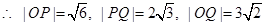
从而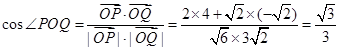
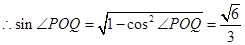 , 10分
, 10分
设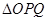 的外接圆的半径为
的外接圆的半径为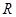 ,
,
由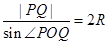
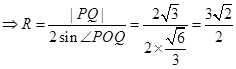
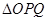 的外接圆的面积
的外接圆的面积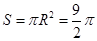 12分
12分
考点:三角函数式的化简,三角函数的性质,正弦定理的应用,圆面积公式.

练习册系列答案
相关题目
 .
.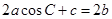 ,求f(B)的取值范围.
,求f(B)的取值范围.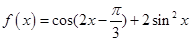 ,
,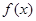 的最大值和最小正周期;
的最大值和最小正周期; 为锐角,且
为锐角,且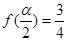 ,求
,求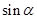 的值.
的值.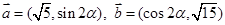 .
.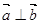 ,且
,且 ,求角
,求角 的值;
的值;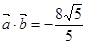 ,且
,且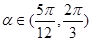 ,求
,求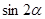 的值.
的值.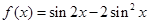
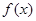 的最小正周期。
的最小正周期。 的图像经过点
的图像经过点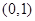 ,
,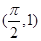 ,当
,当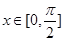 时,恒有
时,恒有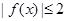 ,求实数
,求实数 的取值范围.
的取值范围. )+
)+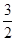 ,x∈R.
,x∈R.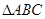 中,角
中,角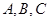 所对的边分别为
所对的边分别为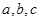 ,且满足
,且满足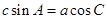 .
.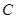 的大小;
的大小;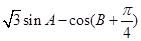 的最大值,并求取得最大值时角
的最大值,并求取得最大值时角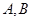 的大小.
的大小. ,且2x+10y=5,则边BC的长
,且2x+10y=5,则边BC的长