题目内容
已知f(x)=sin(-2x+ )+
)+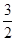 ,x∈R.
,x∈R.
(1)求函数f(x)的最小正周期和单调增区间.
(2)函数f(x)的图象可以由函数y=sin 2x(x∈R)的图象经过怎样的变换得到?
(1) ,
, ;(2)详见解析.
;(2)详见解析.
解析试题分析:(1) ,利用复合函数单调性知:分解为内外层函数
,利用复合函数单调性知:分解为内外层函数 ,求函数的单调递增区间,要求内外层单调性一致,内层为减函数,所以外层也为减函数,所以
,求函数的单调递增区间,要求内外层单调性一致,内层为减函数,所以外层也为减函数,所以 ;
;
(2) 根据左加右减变换到
根据左加右减变换到 ,然后根据上加下减再变换到
,然后根据上加下减再变换到 ,再做关于y轴的对称变换,得到
,再做关于y轴的对称变换,得到 .
.
试题解析:(1)最小正周期为 ,令
,令 ,则
,则 在
在
 上为增函数,即
上为增函数,即 <
< <
< ∴
∴ <
< <
<
 的增区间为
的增区间为
(2)





考点:1. 的性质;2.
的性质;2.  的图像变换.
的图像变换.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
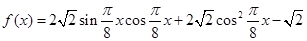 ,
,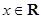 .
.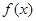 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;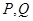 的横坐标依次为
的横坐标依次为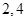 ,
,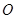 为坐标原点,求
为坐标原点,求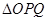 的外接圆的面积.
的外接圆的面积. .
. 的最大值,并写出
的最大值,并写出 的取值集合;
的取值集合; 中,角
中,角 的对边分别为
的对边分别为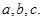 若
若
 求实数
求实数 的最小值.
的最小值.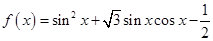 ,
,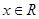 .
.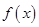 的最小正周期;
的最小正周期; 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为 、
、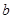 、
、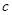 ,且满足
,且满足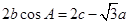 ,求
,求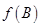 的值.
的值. .
. 的定义域和最小正周期;
的定义域和最小正周期; ,
, ,求
,求 的值.
的值.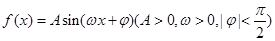 的部分图像如图所示.
的部分图像如图所示.
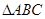 的内角分别是A,B,C.若f(A)=1,
的内角分别是A,B,C.若f(A)=1,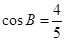 ,求sinC的值.
,求sinC的值.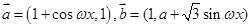 (
(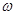 为常数且
为常数且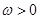 ),函数
),函数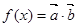 在
在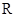 上的最大值为
上的最大值为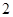 .
.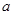 的值;
的值;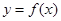 的图象向右平移
的图象向右平移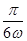 个单位,可得函数
个单位,可得函数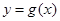 的图象,若
的图象,若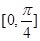 上为增函数,求
上为增函数,求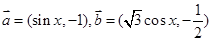 ,函数
,函数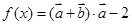 求函数
求函数 的最小正周期T及值域
的最小正周期T及值域 +1)x+m=0的两根为sinθ和cosθ,且θ∈(0,2π).
+1)x+m=0的两根为sinθ和cosθ,且θ∈(0,2π). 的值;
的值;