题目内容
8.已知△ABC中,角A、B、C所对的边分别为a,b,c,且$\frac{a-b}{c}$=$\frac{sinB+sinC}{sinA+sinB}$(1)求A
(2)求cosB+cosC的取值范围.
分析 (1)由正弦定理化简已知等式可得:b2+c2-a2=-bc,由余弦定理可求cosA,结合A∈(0,π),可得A的值.
(2)由(1)得:C=$\frac{π}{3}$-B,利用三角函数恒等变换的应用化简可求cosB+cosC=$\sqrt{3}$sin(B+$\frac{π}{3}$),由B∈(0,$\frac{π}{3}$),可得:B+$\frac{π}{3}$∈($\frac{π}{3}$,$\frac{2π}{3}$),由正弦函数的图象和性质即可得解.
解答 (本题满分为14分)
解:(1)∵$\frac{a-b}{c}$=$\frac{sinB+sinC}{sinA+sinB}$,
∴由正弦定理可得:$\frac{a-b}{c}$=$\frac{b+c}{a+b}$,可得:b2+c2-a2=-bc,
∴由余弦定理可得:cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{-bc}{2bc}$=-$\frac{1}{2}$,
∴由A∈(0,π),可得:A=$\frac{2π}{3}$…6分
(2)∵A=$\frac{2π}{3}$,可得:C=$\frac{π}{3}$-B,
∴cosB+cosC=cosB+cos($\frac{π}{3}$-B)=$\frac{3}{2}$cosB+$\frac{\sqrt{3}}{2}$sinB=$\sqrt{3}$sin(B+$\frac{π}{3}$),
∵B∈(0,$\frac{π}{3}$),可得:B+$\frac{π}{3}$∈($\frac{π}{3}$,$\frac{2π}{3}$),
∴cosB+cosC=$\sqrt{3}$sin(B+$\frac{π}{3}$)∈($\frac{3}{2}$,$\sqrt{3}$]…14分
点评 本题主要考查了正弦定理,余弦定理,三角函数恒等变换的应用,正弦函数的图象和性质在解三角形中的应用,考查了转化思想,属于基础题.

 阅读快车系列答案
阅读快车系列答案| A. | 向右平移$\frac{π}{3}$个单位长度 | B. | 向左平移$\frac{π}{3}$个单位长度 | ||
| C. | 向右平移$\frac{2π}{3}$个单位长度 | D. | 向左平移$\frac{2π}{3}$个单位长度 |
| A. | $({-∞,\frac{1}{4}}]$ | B. | $[{\frac{1}{4},+∞})$ | C. | $[{\frac{1}{2},+∞})$ | D. | $({-∞,\frac{1}{2}}]$ |
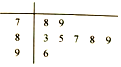
| A. | 86 | B. | 87 | C. | 87.5 | D. | 88.5 |
 如图,三角形ABC中,AB=1,$BC=\sqrt{3}$,以C为直角顶点向外作等腰直角三角形ACD,当∠ABC变化时,线段BD的长度最大值为( )
如图,三角形ABC中,AB=1,$BC=\sqrt{3}$,以C为直角顶点向外作等腰直角三角形ACD,当∠ABC变化时,线段BD的长度最大值为( )| A. | $\sqrt{6}-1$ | B. | $\sqrt{6}$ | C. | $\sqrt{6}+1$ | D. | $2\sqrt{3}$ |
| A. | B⊆A | B. | A∩B=∅ | C. | A∩B={0,1} | D. | A∩B={-2,0,1} |
 如图,直三棱柱的主视图是边长为2的正方形,且俯视图为一个等边三角形,则该三棱柱的左视图面积为2$\sqrt{3}$.
如图,直三棱柱的主视图是边长为2的正方形,且俯视图为一个等边三角形,则该三棱柱的左视图面积为2$\sqrt{3}$.