题目内容
11.椭圆$\frac{x^2}{25}+\frac{y^2}{9}=1$上的一点M到左焦点F1的距离为2,N是MF1的中点,则|ON|等于4.分析 利用椭圆的定义可得|MF2|,再利用三角形中位线定理即可得出.
解答 解:椭圆$\frac{x^2}{25}+\frac{y^2}{9}=1$,
可得a=5,
∴|MF1|+|MF2|=2a=10,
又|MF1|=2,
∴|MF2|=8,
∵N是MF1的中点,O为F1F2的中点,
∴|ON|=$\frac{1}{2}$|MF2|=4.
故答案为:4.
点评 本题考查了椭圆的定义、标准方程及其性质、三角形中位线定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.已知关于x的方程${({\frac{1}{2}})^x}-{x^{\frac{1}{3}}}=0$,那么在下列区间中含有方程的根的是( )
| A. | $(0,\frac{1}{3})$ | B. | $(\frac{1}{3},\frac{1}{2})$ | C. | $(\frac{1}{2},\frac{2}{3})$ | D. | $(\frac{2}{3},1)$ |
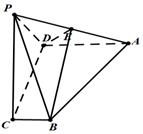 如图所示,四棱锥P-ABCD的底面为一直角梯形,BC⊥CD,CD⊥AD,AD=2BC,PC⊥底面ABCD,E为PA的中点.
如图所示,四棱锥P-ABCD的底面为一直角梯形,BC⊥CD,CD⊥AD,AD=2BC,PC⊥底面ABCD,E为PA的中点.