题目内容
2．设一直角三角形两直角边的长均是区间（0，1）的随机数，则斜边的长小于1的概率为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{3}{4}$ | C． | $\frac{π}{4}$ | D． | $\frac{3π}{16}$ |
分析 设直角三角形的直角边长分别为x，y，则x2+y2＜1，作出平面区域，于是概率等于扇形面积与正方形面积的比值．
解答 
解：设直角三角形的直角边长分别为x，y，则斜边长为$\sqrt{{x}^{2}+{y}^{2}}$＜1．即x2+y2＜1，
作出图形如图所示，则符合条件的x，y落在扇形OAC内部，
∴斜边的长小于1的概率P=$\frac{{S}_{扇形OAC}}{{S}_{正方形OABC}}$=$\frac{π}{4}$．
故选C．
点评 本题考查了几何概率的概率计算，作出平面区域是解题关键，属于基础题．
练习册系列答案
相关题目
13．某种彩票共发行100000张，中奖概率为0.01，则下面说法正确的是（ ）
| A． | 买1张肯定不中奖 | B． | 买100张一定恰有一张能中奖 | ||
| C． | 买100张一定能中奖 | D． | 买100张未必能中奖 |
10．
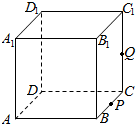如图，正方体ABCD-A1B1C1D1的棱长为1，P为BC的中点，Q为线段CC1上的中点，则四面体A1PQD的正视图、侧视图和俯视图的面积之和为（ ）
如图，正方体ABCD-A1B1C1D1的棱长为1，P为BC的中点，Q为线段CC1上的中点，则四面体A1PQD的正视图、侧视图和俯视图的面积之和为（ ）| A． | $\frac{5}{4}$ | B． | 2 | C． | $\frac{9}{4}$ | D． | $\frac{5}{2}$ |
7．有5名学生的数学和化学成绩如表所示：
（1）如果y与x具有相关关系，求线性回归方程；
（2）预测如果某学生数学成绩为79分，他的化学成绩为多少？
参考公式：：$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$，$\hat a=\overline y-\hat b\overline x$．
| 学生学科 | A | B | C | D | E |
| 数学成绩（x） | 88 | 76 | 73 | 66 | 63 |
| 化学成绩（y） | 78 | 65 | 71 | 64 | 61 |
（2）预测如果某学生数学成绩为79分，他的化学成绩为多少？
参考公式：：$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$，$\hat a=\overline y-\hat b\overline x$．
11．已知a，b∈R，且a＞b，则下列不等式正确的是（ ）
| A． | 2a＞2b | B． | ${（\frac{1}{3}）^a}＞{（\frac{1}{3}）^b}$ | C． | a2＞b2 | D． | lg（a-b）＞0 |
