题目内容
已知α,β表示两个不同的平面,m为平面α内的一条直线,则“α⊥β”是“m⊥β”的 条件(从“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”中选出一种填空.)
考点:充要条件
专题:空间位置关系与距离,简易逻辑
分析:可以想象两平面垂直,平面内的直线和另一平面的位置有:和平面平行,和平面斜交,和平面垂直,在平面内,所以由α⊥β得不出m⊥β,而由m⊥β,能得到α⊥β,这根据面面垂直的判定定理即可得到,所以α⊥β是m⊥β的必要不充分条件.
解答:
解:由m?α,α⊥β得不出m⊥β,因为两平面垂直,其中一平面内的直线可以和另一平面平行;
若m?a,m⊥β,则根据面面垂直的判定定理得到α⊥β;
∴α⊥β,是m⊥β的必要不充分条件.
故答案为必要不充分.
若m?a,m⊥β,则根据面面垂直的判定定理得到α⊥β;
∴α⊥β,是m⊥β的必要不充分条件.
故答案为必要不充分.
点评:考查面面垂直时平面内的直线和另一平面的位置关系,面面垂直的判定定理,以及充分条件、必要条件、必要不充分条件的概念.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知a=(
)0.3,b=0.3-2,c=log
2,则a,b,c的大小关系是( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、a>b>c |
| B、a>c>b |
| C、b>a>c |
| D、c>b>a |
下列函数与y=x有相同图象的一个函数是( )
A、y=
| ||
B、y=
| ||
| C、y=logaax | ||
| D、y=a logax(a>0且a≠1) |
已知函数f(x)由下表给出,则f[f(4)]等于( )
| x | 1 | 2 | 3 | 4 |
| f(x) | 3 | 2 | 4 | 1 |
| A、4 | B、3 | C、2 | D、1 |
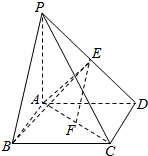 如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AD=1,E,F分别为PA、AC的中点.
如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AD=1,E,F分别为PA、AC的中点.