题目内容
(1-x)4(1-
)3展开式中含x2项的系数为( )
| x |
| A、-3 | B、3 | C、-6 | D、0 |
考点:二项式系数的性质
专题:二项式定理
分析:把所给的式子利用二项式定理展开,可得展开式中含x2项的系数.
解答:
解:由于(1-x)4(1-
)3=(1-4x+6x2-4x3+x4 )(1-3
+3x-x
),
∴展开式中含x2项的系数-4×3+6=-6,
故选:C.
| x |
| x |
| x |
∴展开式中含x2项的系数-4×3+6=-6,
故选:C.
点评:本题主要考查二项式定理的应用,二项展开式的通项公式,二项式系数的性质,属于基础题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
曲线
+
=1与曲线
+
=1(k<9)的( )
| x2 |
| 25 |
| y2 |
| 9 |
| x2 |
| 25-k |
| y2 |
| 9-k |
| A、长轴长相等 | B、短轴长相等 |
| C、离心率相等 | D、焦距相等 |
若有一组数据的总偏差平方和为120,相关指数为0.6,则回归平方和为( )
| A、60 | B、72 | C、48 | D、120 |
正四面体的内切球与外接球的半径的比等于( )
| A、1:3 | B、1:2 |
| C、2:3 | D、3:5 |
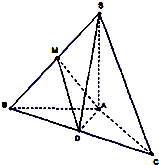 如图,在三棱锥S-ABC中,SA⊥平面ABC,AB=AC=1,SA=2,D为BC的中点.M为SB上的点,且AM=
如图,在三棱锥S-ABC中,SA⊥平面ABC,AB=AC=1,SA=2,D为BC的中点.M为SB上的点,且AM=