题目内容
若关于x的方程2x+
-a=0有正数根，则实数a的取值范围为 ．
| 8 |
| x |
考点：基本不等式
专题：不等式的解法及应用
分析：把方程整理成a=2x+
，利用基本不等式求得其最小值．
| 8 |
| x |
解答：
解：依题意x＞0，
∴a=2x+
≥2
=8，当且仅当2x=
，即x=2时，等号成立．
故a的取值范围是[8，+∞），
故答案为：[8，+∞）．
∴a=2x+
| 8 |
| x |
2x•
|
| 8 |
| x |
故a的取值范围是[8，+∞），
故答案为：[8，+∞）．
点评：本题主要考查了基本不等式的应用．注意“一正，二定，三相等”条件的满足．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
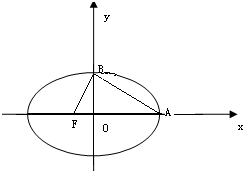已知双曲线的中心在坐标原点，焦点在x轴上，A是右顶点，B是虚轴的上端点，F是左焦点，当BF⊥AB时，此类双曲线称为“黄金双曲线”，其离心率为e=