题目内容
17.已知函数y=sin(x+$\frac{π}{6}$)+sin(x-$\frac{π}{6}$)+2cosx+a的最小值是1,则a的值为$1+\sqrt{7}$.分析 利用两角和与差的正弦展开,再结合辅助角公式化积,由最小值为1列式求得a值.
解答 解:y=sin(x+$\frac{π}{6}$)+sin(x-$\frac{π}{6}$)+2cosx+a=2sinxcosx$\frac{π}{6}$+2cosx+a
=$\sqrt{3}sinx+2cosx+a=\sqrt{{{(\sqrt{3})}^2}+{2^2}}sin(x+φ)+a=\sqrt{7}$sin(x+φ)+a,
根据题意得-$\sqrt{7}$+a=1,解得a=1+$\sqrt{7}$.
故答案为:$1+\sqrt{7}$.
点评 本题考查两角和与差的三角函数,考查了利用辅助角公式求三角函数的最值,是基础题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
7.2015年“双十一”当天,甲、乙两大电商进行了打折促销活动,某公司分别调查了当天在甲、乙电商购物的1000名消费者的消费金额,得到了消费金额的频数分布表如下:
甲电商:
乙电商:
(Ⅰ)根据频数分布表,完成下列频率分布直方图,并根据频率分布直方图比较消费者在甲、乙电商消费金额的中位数的大小以及方差的大小(其中方差大小给出判断即可,不必说明理由);
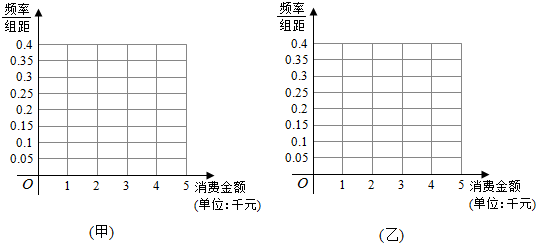
(Ⅱ)
(ⅰ)根据上述数据,估计“双十一”当天在甲电商购物的大量的消费者中,消费金额小于3千元的概率;
(ⅱ)现从“双十一”当天在甲电商购物的大量的消费者中任意调查5位,记消费金额小于3千元的人数为X,试求出X的期望和方差.
甲电商:
| 消费金额(单位:千元) | [0,1) | [1,2) | [2,3) | [3,4) | [4,5] |
| 频数 | 50 | 200 | 350 | 300 | 100 |
| 消费金额(单位:千元) | [0,1) | [1,2) | [2,3) | [3,4) | [4,5] |
| 频数 | 250 | 300 | 150 | 100 | 200 |

(Ⅱ)
(ⅰ)根据上述数据,估计“双十一”当天在甲电商购物的大量的消费者中,消费金额小于3千元的概率;
(ⅱ)现从“双十一”当天在甲电商购物的大量的消费者中任意调查5位,记消费金额小于3千元的人数为X,试求出X的期望和方差.
8.若复数z=$\frac{{{{(1-i)}^2}}}{1+i}$,则|z|=( )
| A. | 8 | B. | 2$\sqrt{2}$ | C. | 2 | D. | $\sqrt{2}$ |
5.设x、y、z是两两不等的实数,且满足下列等式:$\root{6}{{x^3{(y-x)}^3}}+\root{6}{{x^3{(z-x)}^3}}=\root{6}{y-x}-\root{6}{x-z}$,则代数式x3+y3+z3-3xyz的值是( )
| A. | 0 | B. | 1 | ||
| C. | 3 | D. | 条件不足,无法计算 |
12.已知函数$f(x)=sin(ωx+φ)(ω>0,0<φ<\frac{π}{2})$的图象经过点$B(-\frac{π}{6},0)$,且f(x)的相邻两个零点的距离为$\frac{π}{2}$,为得到y=f(x)的图象,可将y=sinx图象上所有点( )
| A. | 先向右平移$\frac{π}{3}$个单位长度,再将所得点的横坐标变为原来的$\frac{1}{2}$倍,纵坐标不变 | |
| B. | 先向左平移$\frac{π}{3}$个单位长度,再将所得点的横坐标变为原来的$\frac{1}{2}$倍,纵坐标不变 | |
| C. | 先向左平移$\frac{π}{3}$个单位长度,再将所得点的横坐标变为原来的2倍,纵坐标不变 | |
| D. | 先向右平移$\frac{π}{3}$个单位长度,再将所得点的横坐标变为原来的2倍,纵坐标不变 |
2.对于任意的整数n(n≥2),满足an=a+1,b2n=b+3a的正数a和b的大小关系是( )
| A. | a>b>1 | B. | b>a>1 | C. | a>1,0<b<1 | D. | 0<a<1,b>1 |
6.若实数x,y满足$\left\{\begin{array}{l}{x-y+5≥0}\\{x+y≥0}\\{x≤3}\end{array}\right.$,则z=$\sqrt{{x}^{2}+{y}^{2}}$的最大值是( )
| A. | $\sqrt{43}$ | B. | $\frac{5\sqrt{2}}{2}$ | C. | $\sqrt{73}$ | D. | 3$\sqrt{2}$ |
7.设数列{an}满足:a1=1,a2=3,且2nan=(n-1)an-1+(n+1)an+1,则a20的值是( )
| A. | 4$\frac{1}{5}$ | B. | 4$\frac{2}{5}$ | C. | 4$\frac{3}{5}$ | D. | 4$\frac{4}{5}$ |