题目内容
1.甲、乙两人约定晚上6点到7点之间在某地见面,并约定先到者要等候另一人10分钟,过时即可离开.则甲、乙能见面的概率为$\frac{11}{36}$.分析 由题意知本题是一个几何概型,试验包含的所有事件是Ω={(x,y)|0≤x≤60,0≤y≤60},求出事件对应的集合表示的面积,写出满足条件的事件,算出事件对应的集合表示的面积,根据几何概型概率公式得到结果.
解答 解:设事件A为“两人能会面”,以7点钟作为计算时间的起点,
设甲乙各在第x分钟和第y分钟到达
试验包含的所有事件是Ω={(x,y)|0≤x≤60,0≤y≤60},
并且事件对应的集合表示的面积是S=60×60=3600,
满足条件的事件是A={(x,y)|0≤x≤60,0≤y≤60,|x-y|<10}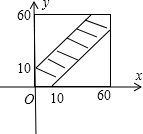
所以事件对应的集合表示的面积是3600-2×$\frac{1}{2}$×50×50=1100,
根据几何概型概率公式得到P=$\frac{1100}{3600}$=$\frac{11}{36}$
故答案为:$\frac{11}{36}$
点评 本题是一个几何概型,对于这样的问题,一般要通过把试验发生包含的事件同集合结合起来,根据集合对应的图形做出面积,用面积的比值得到结果.

练习册系列答案
相关题目
11. 已知△ABC中,$AB=1,BC=\sqrt{3},BD$是AC边上的中线.
已知△ABC中,$AB=1,BC=\sqrt{3},BD$是AC边上的中线.
(1)求$\frac{sin∠ABD}{sin∠CBD}$;
(2)若$∠A=\frac{2π}{3}$,求BD的长.
 已知△ABC中,$AB=1,BC=\sqrt{3},BD$是AC边上的中线.
已知△ABC中,$AB=1,BC=\sqrt{3},BD$是AC边上的中线.(1)求$\frac{sin∠ABD}{sin∠CBD}$;
(2)若$∠A=\frac{2π}{3}$,求BD的长.
12.过点P(-2,0)的双曲线C与椭圆$\frac{x^2}{25}+\frac{y^2}{9}=1$的焦点相同,则双曲线C的渐近线方程是( )
| A. | $y=±\frac{{\sqrt{3}}}{3}x$ | B. | $y=±\sqrt{3}x$ | C. | $y=±\frac{1}{2}x$ | D. | y=±2x |
16.已知$sin(θ-\frac{π}{4})=\frac{1}{5}$,则$cos(θ+\frac{π}{4})$=( )
| A. | $-\frac{1}{5}$ | B. | $\frac{1}{5}$ | C. | $-\frac{{2\sqrt{2}}}{5}$ | D. | $\frac{{2\sqrt{2}}}{5}$ |
13.当实数m分别取什么值时,复数z=(m2+5m+6)+(m2-2m-15)i不是纯虚数( )
| A. | m≠5 | B. | m≠3 | C. | m≠-2 | D. | m≠-3 |
15.函数 f(x)=2x+x,则 ( )
| A. | f(1)>f(2) | B. | f(π)<f(3) | C. | $f(\sqrt{e})<f(1.5)$ | D. | f(1.10.5)>f(log32) |
 已知三棱锥S-ABC,底面△ABC为边长为2的正三角形,侧棱SA=SC=$\sqrt{2}$,SB=2
已知三棱锥S-ABC,底面△ABC为边长为2的正三角形,侧棱SA=SC=$\sqrt{2}$,SB=2