题目内容
7．若抛物线y2=-16x上一点P到x轴的距离为12，则该点到焦点的距离为（ ）| A． | 5 | B． | 8 | C． | -5 | D． | 13 |
分析 先把点P的纵坐标代入抛物线方程求得点P的横坐标，进而根据抛物线的定义求得答案．
解答 解：依题意可知点P的纵坐标|y|=12，代入抛物线方程求得x=-9
抛物线的准线为x=4，
根据抛物线的定义可知点P与焦点F间的距离4+9=13
故选：D．．
点评 本题考查抛物线的方程与定义，考查学生的计算能力，正确运用抛物线的定义是关键．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
15．边长为4$\sqrt{3}$的等边△ABC中，D为边AB的中点，若P为线段CD的中点，则（$\overrightarrow{PA}$+$\overrightarrow{PB}$）•$\overrightarrow{PC}$的值为（ ）
| A． | 18 | B． | -18 | C． | 2$\sqrt{3}$ | D． | -2$\sqrt{3}$ |
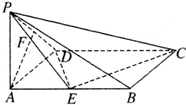已知在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=1，AB=2，E，F分别是AB，PD的中点．