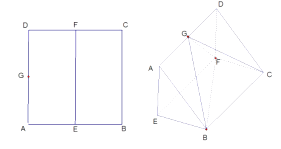
题目内容
【题目】已知三棱锥 ![]() ,底面
,底面 ![]() 是以
是以 ![]() 为直角顶点的等腰直角三角形,
为直角顶点的等腰直角三角形, ![]() ,
, ![]() ,二面角
,二面角 ![]() 的大小为
的大小为 ![]() .
.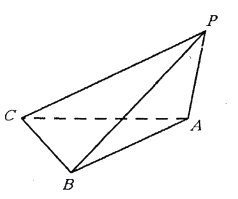
(1)求直线 ![]() 与平面
与平面 ![]() 所成角的大小;
所成角的大小;
(2)求二面角 ![]() 的正切值.
的正切值.
【答案】
(1)解:过点 ![]() 作
作 ![]() 底面
底面 ![]() 垂足为
垂足为 ![]() ,
,
连接 ![]() ,则∠
,则∠ ![]() 为所求线面角,
为所求线面角,![]()
![]() ,
,![]() 平面
平面 ![]() .则
.则 ![]() 为二面角
为二面角 ![]() 平面角的补角
平面角的补角
∴∠ ![]() ,又
,又 ![]() ,
, ![]()
![]() ,直线
,直线 ![]() 与面
与面 ![]() 所成角的大小为
所成角的大小为 ![]() .
.
(2)解:过 ![]() 作
作 ![]() 于点
于点 ![]() ,连接
,连接 ![]() ,则
,则 ![]() 为二面角
为二面角 ![]() 的平面角,
的平面角,![]() 平面
平面 ![]() ,
, ![]()
![]() ,
,
设 ![]() 与
与 ![]() 相交于
相交于 ![]()
![]() ,
,
在 ![]() 中,
中, ![]()
则二面角 ![]() 的正切值为
的正切值为 ![]() .
.
【解析】(1)直线与平面所成的角就是直线在平面内的射影与直线所成的角,已知的二面角体现图形中的数量关系,找到线面角,在三角形中求得角.
(2)找到所求二面角的一个平面角,再在直角三角形中,解三角形求角.
【考点精析】解答此题的关键在于理解空间角的异面直线所成的角的相关知识,掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 .
.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目