��Ŀ����
����Ŀ��
Ϊ�˱�����������չ��̼���ã�ij��λ���������ŵ�֧���£����м������أ��������¹��գ������˰Ѷ�����̼ת��Ϊһ�ֿ����õĻ�����Ʒ����Ŀ.�����㣬�´����ɱ�![]() ��Ԫ�����´�����
��Ԫ�����´�����![]() ���֣�֮��ĺ�����ϵ���Խ��Ƶı�ʾΪ��
���֣�֮��ĺ�����ϵ���Խ��Ƶı�ʾΪ�� ����ÿ����һ�ֶ�����̼�ɵõ������õĻ�����Ʒ��ֵΪ200Ԫ��������Ŀ������������������.
����ÿ����һ�ֶ�����̼�ɵõ������õĻ�����Ʒ��ֵΪ200Ԫ��������Ŀ������������������.
��I����![]() ʱ���жϸ���Ŀ�ܷ������������������������������������������ÿ��������Ҫ��������Ԫ����ʹ����Ŀ������
ʱ���жϸ���Ŀ�ܷ������������������������������������������ÿ��������Ҫ��������Ԫ����ʹ����Ŀ������
��II������Ŀÿ�´�����Ϊ���ٶ�ʱ������ʹÿ�ֵ�ƽ�������ɱ���ͣ�
���𰸡���I���貹��![]() ����II��
����II��![]() .
.
��������
�����������I����![]() ʱ��������
ʱ��������![]() ��������
��������![]() �����߲��Ƕ��κ��������䷽����֪����Ŀ�����������II��ƽ�������ɱ���
�����߲��Ƕ��κ��������䷽����֪����Ŀ�����������II��ƽ�������ɱ���![]() ����
����![]() ʱ��
ʱ��![]() �����Ե�
�����Ե�![]() ʱ��
ʱ��![]() ȡ����Сֵ
ȡ����Сֵ![]() . ��
. ��![]() ʱ��
ʱ��![]() ����ÿ�´�����Ϊ
����ÿ�´�����Ϊ![]() ��ʱ������ʹÿ�ֵ�ƽ�������ɱ����.
��ʱ������ʹÿ�ֵ�ƽ�������ɱ����.
���������
��I����![]() ʱ�������Ŀ����Ϊ
ʱ�������Ŀ����Ϊ![]() ����
����
![]()
![]()
���Ե�![]() ʱ��
ʱ��![]() ����ˣ�����Ŀ���������
����ˣ�����Ŀ���������
��![]() ʱ��
ʱ��![]() ȡ�����ֵ
ȡ�����ֵ![]() ��
��
��������ÿ��������Ҫ����5000Ԫ����ʹ����Ŀ������
��2���������֪��ʳƷ������ÿ��ƽ�������ɱ�Ϊ��
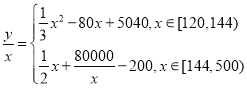 ��
��
�� ��![]() ʱ��
ʱ��![]() ��
��
���Ե�![]() ʱ��
ʱ��![]() ȡ����Сֵ240. 9��
ȡ����Сֵ240. 9��
�� ��![]() ʱ��
ʱ��
![]() ��
��
���ҽ���![]() ����
����![]() ʱ��
ʱ��![]() ȡ����Сֵ200����Ϊ200<400�����Ե�ÿ�´�����Ϊ400��ʱ������ʹÿ�ֵ�ƽ�������ɱ����.
ȡ����Сֵ200����Ϊ200<400�����Ե�ÿ�´�����Ϊ400��ʱ������ʹÿ�ֵ�ƽ�������ɱ����.