题目内容
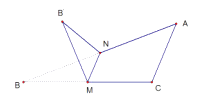
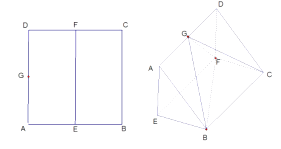
【题目】如图所示，正方体 
中， 
分别是 
的中点，将 沿 
折起，使 
.
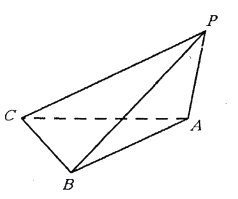
（1）证明： 
平面 
；
（2）求二面角 
的余弦值.
【答案】
（1）证明：设正方体的棱长为2，
在 
中， 
， 
，所以 
，
∵ 
， 
，
∴ 
平面 
，∵ 
，∴ 
平面 ，∴ 
，
所以在 中，得 
在 
中，又 
，∴ 
又 ，∴ 
平面 
.
（2）解：取 
的中点 
，则 
，由（1）知， 平面 .
所以平面 
平面 ，所以 
平面 
，作 
，垂足为 
，连接 
，
由三垂线定理知， 
，
所以 
就是所求二面角 
的平面角.
在 
中， 
， 
，
所以 
，所以 
，
所以二面角 的余弦值为 
.
【解析】(1)平面图形的翻折问题中,要注意哪些因素改变,哪些因素不改变,由直线与平面图内两条相交直线都有垂直证明直线与平面垂直.
(2)先由二面角的定义找互二面角的一个平面图角,再在三角形中,通过解三角形求角.
练习册系列答案
相关题目
