题目内容
20.已知正项数列{an}的前n项和为Sn,且Sn,an,$\frac{1}{2}$成等差数列.(1)求数列{an}的通项公式an;
(2)若bn=log2an+3,求数列$\left\{{\frac{1}{{{b_n}{b_{n+1}}}}}\right\}$的前n项和为Tn.
分析 (1)由题知:$2{a_n}={S_n}+\frac{1}{2}$,利用递推关系、等比数列的通项公式即可得出.
(2)bn=n+1,$\frac{1}{{{b_n}{b_{n+1}}}}=\frac{1}{{({n+1})({n+2})}}=\frac{1}{n+1}-\frac{1}{n+2}$,利用“裂项求和”即可得出.
解答 解:(1)由题知:$2{a_n}={S_n}+\frac{1}{2}$,∴$2{a_{n-1}}={S_{n-1}}+\frac{1}{2}({n≥2})$,
两式相减,化简得:an=2an-1(n≥2),
故{an}是等比数列,且公比q=2,而n=1时,${a_1}=\frac{1}{2}$.
∴${a_n}=\frac{1}{2}•{2^{n-1}}={2^{n-2}}$.
(2)bn=n+1,$\frac{1}{{{b_n}{b_{n+1}}}}=\frac{1}{{({n+1})({n+2})}}=\frac{1}{n+1}-\frac{1}{n+2}$,
∴Tn=$(\frac{1}{2}-\frac{1}{3})$+$(\frac{1}{3}-\frac{1}{4})$+…+$(\frac{1}{n+1}-\frac{1}{n+2})$=$\frac{1}{2}-\frac{1}{n+2}$.
点评 本题考查了递推关系、等比数列的通项公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
11.执行如图所示的程序框图,若输出的$S=\frac{25}{24}$,则判断框内填入的条件可以是( )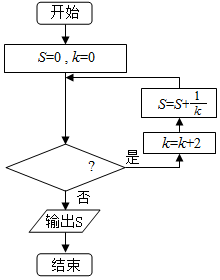

| A. | k≥7 | B. | k>7 | C. | k≤8 | D. | k<8 |
5.在n元数集S={a1,a2,…an}中,设X(S)=$\frac{{a}_{1}+{a}_{2}+…+{a}_{n}}{n}$,若S的非空子集A满足X(A)=X(S),则称A是集合S的一个“平均子集”,并记数集S的k元“平均子集”的个数为fs(k),已知集合S={1,2,3,4,5,6,7,8,9},T={-4,-3,-2,-1,0,1,2,3,4},则下列说法错误的是( )
| A. | fs(4)=fs(5) | B. | fs(4)=fT(5) | C. | fs(1)+fs(4)=fT(5)+fT(8) | D. | fs(2)+fs(3)=fT(4) |