题目内容
已知函数f(x)=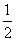 λsin ωx+
λsin ωx+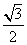 λcos ωx(λ>0,ω>0)的部分图象如图所示,其中点A为最高点,点B,C为图象与x轴的交点,在△ABC中,角A,B,C的对边分别为a,b,c,b=c=
λcos ωx(λ>0,ω>0)的部分图象如图所示,其中点A为最高点,点B,C为图象与x轴的交点,在△ABC中,角A,B,C的对边分别为a,b,c,b=c= ,且满足(2c-
,且满足(2c- a)cos B-
a)cos B- bcos A=0.
bcos A=0.
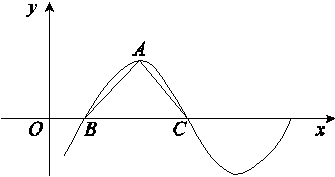
(1)求△ABC的面积;
(2)求函数f(x)的单调递增区间.
解:(1)由(2c- a)cos B-
a)cos B- bcos A=0,得B=
bcos A=0,得B= .
.
在△ABC中,BC边上的高h=csin B=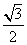 ,BC=2ccos B=3,
,BC=2ccos B=3,
故S△ABC=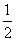 ×BC×h=
×BC×h=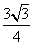 .
.
(2)f(x)=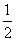 λsin ωx+
λsin ωx+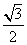 λcos ωx
λcos ωx
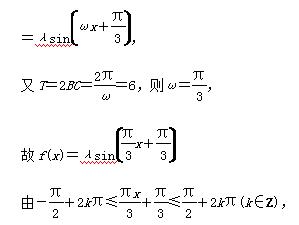 可得6k-
可得6k-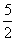 ≤x≤6k+
≤x≤6k+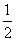 (k∈Z).
(k∈Z).
所以函数f(x)的单调递增区间为
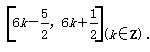

练习册系列答案
相关题目
 在区间
在区间 上存在反函数,则实数
上存在反函数,则实数 的取值范围是---------
的取值范围是---------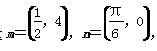 ,点P在y=cos x的图象上运动,点Q在y=f(x)的图象上运动,且满足
,点P在y=cos x的图象上运动,点Q在y=f(x)的图象上运动,且满足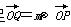 +n(其中O为坐标原点),则y=f(x)在区间
+n(其中O为坐标原点),则y=f(x)在区间 上的最大值是( )
上的最大值是( )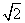 D.2
D.2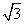
 ,b=2acos B,c=1,则△ABC的面积等于( )
,b=2acos B,c=1,则△ABC的面积等于( )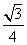 C.
C.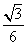 D.
D.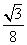
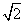 C.3 D.
C.3 D.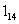 01)2转换成十进制数是( )
01)2转换成十进制数是( )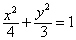 的离心率为 ( )
的离心率为 ( )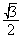 B.
B.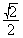 C.
C. D.
D.