题目内容
若无穷数列 满足:①对任意
满足:①对任意 ,
, ;②存在常数
;②存在常数 ,对任意
,对任意 ,
, ,则称数列
,则称数列 为“
为“ 数列”.
数列”.
(Ⅰ)若数列 的通项为
的通项为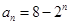
 ,证明:数列
,证明:数列 为“
为“ 数列”;
数列”;
(Ⅱ)若数列 的各项均为正整数,且数列
的各项均为正整数,且数列 为“
为“ 数列”,证明:对任意
数列”,证明:对任意 ,
, ;
;
(Ⅲ)若数列 的各项均为正整数,且数列
的各项均为正整数,且数列 为“
为“ 数列”,证明:存在
数列”,证明:存在 ,数列
,数列 为等差数列.
为等差数列.
 满足:①对任意
满足:①对任意 ,
, ;②存在常数
;②存在常数 ,对任意
,对任意 ,
, ,则称数列
,则称数列 为“
为“ 数列”.
数列”.(Ⅰ)若数列
 的通项为
的通项为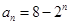
 ,证明:数列
,证明:数列 为“
为“ 数列”;
数列”;(Ⅱ)若数列
 的各项均为正整数,且数列
的各项均为正整数,且数列 为“
为“ 数列”,证明:对任意
数列”,证明:对任意 ,
, ;
;(Ⅲ)若数列
 的各项均为正整数,且数列
的各项均为正整数,且数列 为“
为“ 数列”,证明:存在
数列”,证明:存在 ,数列
,数列 为等差数列.
为等差数列.(Ⅰ)详见解析;(Ⅱ)详见解析;(Ⅲ)详见解析
试题分析:(Ⅰ)用作差法证
 ,用单调性证
,用单调性证 。(Ⅱ)用反证法证明。即假设存在正整数
。(Ⅱ)用反证法证明。即假设存在正整数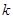 ,使得
,使得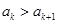 。根据
。根据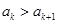 和
和 结合放缩法推倒论证得出与已知各项均为正整数相矛盾,则说明假设不成立即原命题成立。(Ⅲ)由(Ⅱ)知
结合放缩法推倒论证得出与已知各项均为正整数相矛盾,则说明假设不成立即原命题成立。(Ⅲ)由(Ⅱ)知 ,需分
,需分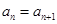 和
和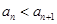 两种情况讨论,结合已知
两种情况讨论,结合已知 推理论证,根据等差的定义可证得存在
推理论证,根据等差的定义可证得存在  ,数列
,数列 为等差数列.本题的关键是当
为等差数列.本题的关键是当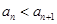 可变形得
可变形得 ,再用累加法表示
,再用累加法表示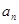 ,即
,即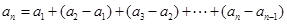 ,根据
,根据 进行推理论证。
进行推理论证。试题解析:(Ⅰ)证明:由
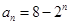 ,可得
,可得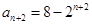 ,
,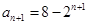 ,
,所以
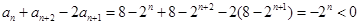 ,
,所以对任意
 ,
, .
.又数列
 为递减数列,所以对任意
为递减数列,所以对任意 ,
,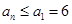 .
.所以数列
 为“
为“ 数列”. 5分
数列”. 5分(Ⅱ)证明:假设存在正整数
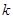 ,使得
,使得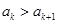 .
.由数列
 的各项均为正整数,可得
的各项均为正整数,可得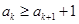 .
.由
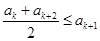 ,可得
,可得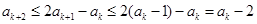 .
.且
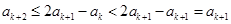 .
.同理
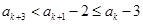 ,
,依此类推,可得,对任意
 ,有
,有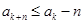 .
.因为
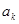 为正整数,设
为正整数,设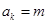 ,则
,则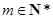 .
.在
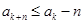 中,设
中,设 ,则
,则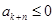 .
.与数列
 的各项均为正整数矛盾.
的各项均为正整数矛盾.所以,对任意
 ,
, . 10分
. 10分(Ⅲ)因为数列
 为“
为“ 数列”,
数列”,所以,存在常数
 ,对任意
,对任意 ,
, .
.设
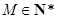 .
.由(Ⅱ)可知,对任意
 ,
, ,
,则
 .
.若
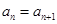 ,则
,则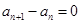 ;若
;若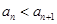 ,则
,则 .
.而
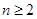 时,有
时,有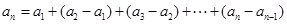 .
.所以
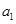 ,
,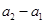 ,
,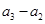 ,
,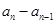 ,中最多有
,中最多有 个大于或等于
个大于或等于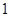 ,
,否则与
 矛盾.
矛盾.所以,存在
 ,对任意的
,对任意的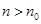 ,有
,有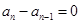 .
.所以,对任意
 ,
, .
.所以,存在
 ,数列
,数列 为等差数列. 14分
为等差数列. 14分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
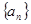 满足:
满足: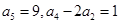 .
. 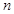 项和
项和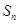 ;
;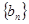 的前
的前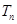 ,且
,且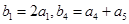 ,求
,求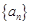 、
、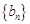 的每一项都是正数,
的每一项都是正数,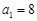 ,
,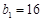 ,且
,且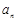 、
、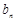 、
、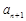 成等差数列,
成等差数列,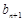 成等比数列,
成等比数列,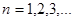 .
.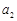 、
、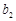 的值;
的值;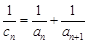 ,证明:对一切正整数
,证明:对一切正整数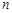 ,有
,有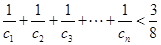 .
.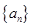 的前
的前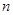 项和为
项和为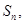 记
记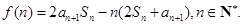
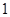 的等差数列,求
的等差数列,求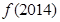 ;
; 且数列
且数列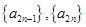 均是公比为
均是公比为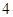 的等比数列,
的等比数列,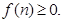
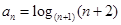
 .我们把使乘积
.我们把使乘积 为整数的数n叫做“优数”,则在区间(1,2004)内的所有优数的和为( )
为整数的数n叫做“优数”,则在区间(1,2004)内的所有优数的和为( ) 满足:
满足: ,
, 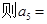 ( )
( )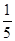

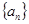 中,若
中,若 ,
,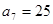 ,则公差
,则公差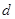 等于( )
等于( )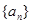 的前
的前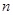 项和记为
项和记为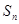 ,若
,若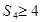 ,
,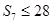 ,则
,则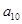 的最大值为 .
的最大值为 .