题目内容
已知向量
=(2cosx+1,cos2x-sinx+1),
=(cosx,-1),f(x)=
•
(1)求函数f(x)最小正周期;
(2)当x∈[0,
],求函数f(x)的最大值及取得最大值时的x.
| OP |
| OQ |
| OP |
| OQ |
(1)求函数f(x)最小正周期;
(2)当x∈[0,
| π |
| 2 |
考点:三角函数的周期性及其求法,平面向量数量积的运算
专题:三角函数的图像与性质
分析:(1)由条件利用两个向量的数量积公式,三角函数的恒等变换求得f(x)=
sin(x+
),从而得到它的最小正周期.
(2)由条件利用正弦函数的定义域和值域,求得f(x)的最大值.
| 2 |
| π |
| 4 |
(2)由条件利用正弦函数的定义域和值域,求得f(x)的最大值.
解答:
解:(1)∵f(x)=
•
=cosx(2cosx+1)-(cos2x-sinx+1)=2cos2x+cosx-cos2x+sinx-1
=cosx+sinx=
sin(x+
),
∴函数f(x)最小正周期为
=2π.
(2)又x∈[0,
],所以x+
∈[
,
],函数f(x)=
sin(x+
)在[
,
]上单调递增,在[
,
]上单调递减,
故当x=
时,f(x)取得最大值为
.
| OP |
| OQ |
=cosx+sinx=
| 2 |
| π |
| 4 |
∴函数f(x)最小正周期为
| 2π |
| 1 |
(2)又x∈[0,
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
| 3π |
| 4 |
故当x=
| π |
| 4 |
| 2 |
点评:本题主要考查两个向量的数量积公式,三角函数的恒等变换及化简求值,正弦函数的定义域和值域,属于基础题.

练习册系列答案
相关题目
执行如图的程序框图,若输出的n=5,则输入整数p的最小值是( )


| A、6 | B、7 | C、8 | D、15 |
如图所示的程序框图表示求算式“2×4×8×16×32”的值,则判断框内可以填入( )
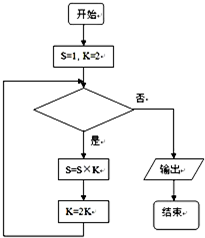

| A、k<10 | B、k<20 |
| C、k<30 | D、k<40 |
已知{an}为等差数列,且a2=3,a6=5,S7=( )
| A、42 | B、28 | C、24 | D、34 |
计算|
|=( )
| i-1 |
| i+1 |
| A、i | B、-i | C、1 | D、-1 |