${∫} {1}^{e}$dx=( )A．e2B．$\frac{{e}^{2}+1}{2}$C．$\frac{{e}^{2}-1}{2}$D．$\frac{{e}^{2}+3}{2}$ 题目和参考答案——青夏教育精英家教网—

题目内容

14．${∫}_{1}^{e}$（x+$\frac{1}{x}$）dx=（　　）

A．

e²

B．

$\frac{{e}^{2}+1}{2}$

C．

$\frac{{e}^{2}-1}{2}$

D．

$\frac{{e}^{2}+3}{2}$

分析根据定积分的计算法则计算即可．

解答解：${∫}_{1}^{e}$（x+$\frac{1}{x}$）dx=（$\frac{1}{2}$x²+lnx）|${\;}_{1}^{e}$=（$\frac{1}{2}$e²+1）-（$\frac{1}{2}$+0）=$\frac{{e}^{2}+1}{2}$，
故选：B

点评本题考查了定积分的计算，属于基础题．

练习册系列答案

相关题目

2．设P={x|x＜4}，Q={x|x²＜4}，则（　　）

5．设函数f（x）=$\left\{\begin{array}{l}{（\frac{1}{3}）^{-x}-2，x≥0}\\{2lo{g}_{3}（-x），x＜0}\end{array}\right.$若f（m）＞1，则m的取值范围是（　　）

（-∞，-$\sqrt{3}$）∪（1，+∞）

D．

（-∞，-$\sqrt{3}$）

2．

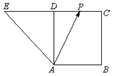如图，四边形ABCD是正方形，延长CD至E，使得DE=CD，若点P为CD的中点，且$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$，则λ+μ=（　　）

9．已知数列{a_n}满足a₁=1，a_n+1=2a_n+1（n∈N^*）．若数列{b_n}满足：4${\;}^{{b_1}-1}}$•4${\;}^{{b_2}-1}}$•…4${\;}^{{b_n}-1}}$=（a_n+1）^b_n（n∈N^*）．
（1）求数列{a_n}的通项公式；
（2）求证：{b_n}是等差数列．

19．设f（x）=ax²-a+$\frac{e}{{e}^{x}}$，g（x）=$\frac{1}{x}$+lnx．
（Ⅰ）设h（x）=f（x）-g（x）+$\frac{{e}^{x}-ex}{x{e}^{x}}$，讨论y=h（x）的单调性；
（Ⅱ）证明：对任意a∈（-∞，$\frac{1}{2}$），?x∈（1，+∞），使f（x）＜g（x）成立．

6．已知椭圆Γ的中心在原点，焦点在x轴，离心率为$\frac{{\sqrt{2}}}{2}$，且长轴长是短轴长的$\sqrt{2}$倍．
（1）求椭圆Γ的标准方程；
（2）设P（2，0）过椭圆Γ左焦点F的直线l交Γ于A，B两点，若对满足条件的任意直线l，不等式$\overrightarrow{PA}•\overrightarrow{PB}≤λ（{λ∈R}）$恒成立，求λ的最小值．

3．设?x?表示不小于实数x的最小整数，如?2.6?=3，?-3.5?=-3．已知函数f（x）=?x?²-2?x?，若函数F（x）=f（x）-k（x-2）+2在（-1，4]上有2个零点，则k的取值范围是（　　）

A．

$[{-\frac{5}{2}，-1}）∪[2，5）$

B．

$（{-\frac{4}{3}，-1}]∪[5，10）$

C．

$[{-1，-\frac{2}{3}}）∪[5，10）$

D．

$[{-\frac{4}{3}，-1}]∪[5，10）$

4．已知椭圆 C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左，右焦点分别是F₁，F₂，点 D 在椭圆 C 上，DF₁⊥F₁F₂，|F₁F₂|=4$\sqrt{3}$|DF|，△DFF的面积为$\frac{{\sqrt{3}}}{2}$．
（1）求椭圆C的方程；（2）圆x²+y²=b²的切线l交椭圆C于A，B两点，求|AB|的最大值．

试题分类