题目内容
2.若曲线$\frac{x^2}{4-m}+\frac{y^2}{13-m}=1$表示双曲线,则焦点坐标为(0,±3).分析 曲线$\frac{x^2}{4-m}+\frac{y^2}{13-m}=1$表示双曲线,可得(4-m)(13-m)<0,焦点在y轴上,且c2=13-m+m-4=9,即可求出焦点坐标.
解答 解:∵曲线$\frac{x^2}{4-m}+\frac{y^2}{13-m}=1$表示双曲线,
∴(4-m)(13-m)<0,
∴4<m<13.
∴焦点在y轴上,且c2=13-m+m-4=9,
∴焦点坐标为(0,±3).
故答案为:(0,±3).
点评 本题考查双曲线的方程与性质,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
12.已知定义域为R的函数f(x)以4为周期,且函数f(x)=$\left\{\begin{array}{l}{\sqrt{1-{x}^{2}},x∈(-1,1]}\\{2-|x-2|,x∈(1,3]}\end{array}\right.$,若满足函数g(x)=f(x)-mx(m>0)恰有5个零点,则m的取值范围为( )
| A. | ($\frac{\sqrt{15}}{15}$,$\frac{1}{3}$) | B. | [$\frac{1}{5}$,$\frac{\sqrt{15}}{15}$) | C. | ($\frac{1}{5}$,$\frac{\sqrt{15}}{15}$] | D. | ($\frac{1}{7}$,$\frac{1}{5}$] |
10.直线y=k(x-3)与双曲线$\frac{x^2}{9}-\frac{y^2}{4}=1$只有一个公共点,则k的值有( )
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 无数个 |
7.已知函数f(x)=|sinx|+|cosx|,则下列结论中错误的是( )
| A. | f(x)是周期函数 | B. | f(x)的对称轴方程为x=$\frac{kπ}{4}$,k∈Z | ||
| C. | f(x)在区间($\frac{π}{4}$,$\frac{3π}{4}$)上为增函数 | D. | 方程f(x)=$\frac{6}{5}$在区间[-$\frac{3}{2}$π,0]上有6个根 |
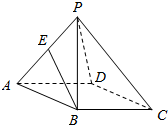 如图,在底面为正方形的四棱锥P-ABCD中,PA=PB=PC=PD=AB=2,点E为棱PA的中点,则异面直线BE与PD所成角的余弦值为$\frac{\sqrt{3}}{6}$.
如图,在底面为正方形的四棱锥P-ABCD中,PA=PB=PC=PD=AB=2,点E为棱PA的中点,则异面直线BE与PD所成角的余弦值为$\frac{\sqrt{3}}{6}$.