题目内容
已知数列:1,2,2,4,8,32,…,写出这个数列的一个递推公式.
考点:数列的概念及简单表示法
专题:等差数列与等比数列
分析:由数列:1,2,2,4,8,32,…,可得:从第3项起,每一项是前两项的乘积,即可得出.
解答:
解:由数列:1,2,2,4,8,32,…,可得这个数列的一个递推公式a1=1,a2=2,an+2=anan+1.
点评:本题考查了递推式的求法,属于基础题.

练习册系列答案
相关题目
已知函数f(x)=2x2-ax-1,在[-1,2]上单调,则实数a的取值范围是( )
| A、[-4,8] |
| B、(-∞,-4] |
| C、[8,+∞] |
| D、(-∞,-4]∪[8,+∞) |
定义表示不超过x的最大整数[x],记{x}=x-[x],二次函数y=-x2+mx-2与函数y={-x}在(-1,0]上有两个不同的交点,则m的取值范围是( )
A、(-
| ||||
B、(
| ||||
| C、∅ | ||||
| D、以上均不正确 |
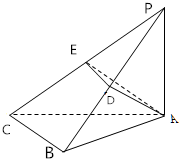 如图,PA⊥平面ABC,AB⊥BC,AD⊥PB,AE⊥PC,AP=
如图,PA⊥平面ABC,AB⊥BC,AD⊥PB,AE⊥PC,AP=