题目内容
13.3位同学各自参加甲、乙两个兴趣小组,则两个兴趣小组都有同学参加的概率是( )| A. | $\frac{3}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{7}{9}$ | D. | $\frac{3}{4}$ |
分析 3位同学各自参加甲、乙两个兴趣小组,基本事件有23=8种,其中仅参加一个兴趣小组的各有一种,根据古典概型概率公式得到结果.
解答 解:3位同学各自参加甲、乙两个兴趣小组的情况有8种方式,其中仅参加一个兴趣小组的各有一种,
故所求概率$p=1-\frac{1+1}{8}=\frac{3}{4}$.
故选:D.
点评 本题考查古典概型概率公式,是一个基础题,题目使用列举法来得到试验发生包含的事件数和满足条件的事件数,出现这种问题一定是一个必得分题目.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
3.设双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左、右焦点分别为F1,F2.若左焦点F1关于其中一条渐近线的对称点位于双曲线上,则该双曲线的离心率e的值为( )
| A. | $\sqrt{3}$ | B. | 3 | C. | $\sqrt{5}$ | D. | 5 |
2.i是虚数单位,满足(1+2i)z=-3+4i的复数z=( )
| A. | 1-2i | B. | -$\frac{11}{5}$+2i | C. | 1+2i | D. | -4+2i |
3.已知集合A=$\{x|y=\sqrt{x-1}\}$,B={x|y=ln(2x-x2)},则A∩B=( )
| A. | (2,+∞) | B. | [1,2) | C. | (0,2) | D. | [1,2] |
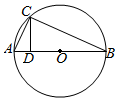 圆O上一点C在直径AB上的射影为D,AD=4,DB=8,求CD,AC和BC的长.
圆O上一点C在直径AB上的射影为D,AD=4,DB=8,求CD,AC和BC的长.