题目内容
10.已知△ABC的外接圆圆心为O,半径R=1,且2$\overrightarrow{OA}$+3$\overrightarrow{OB}$+4$\overrightarrow{OC}$=$\overrightarrow 0$,则AC=$\frac{{3\sqrt{6}}}{4}$.分析 可以由$2\overrightarrow{OA}+3\overrightarrow{OB}+4\overrightarrow{OC}=\overrightarrow{0}$得到$2\overrightarrow{OA}+4\overrightarrow{OC}=-3\overrightarrow{OB}$,根据条件两边平方,进行数量积的运算便可得到$\overrightarrow{OA}•\overrightarrow{OC}=-\frac{11}{16}$,而$\overrightarrow{AC}=\overrightarrow{OC}-\overrightarrow{OA}$,两边平方即可求出${\overrightarrow{AC}}^{2}$,进而得出$|\overrightarrow{AC}|$的值,即AC的值.
解答 解:如图,由题意得:$|\overrightarrow{OA}|=|\overrightarrow{OB}|=|\overrightarrow{OC}|=1$;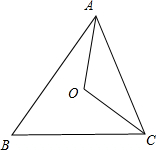
由$2\overrightarrow{OA}+3\overrightarrow{OB}+4\overrightarrow{OC}=\overrightarrow{0}$得,$2\overrightarrow{OA}+4\overrightarrow{OC}=-3\overrightarrow{OB}$,两边平方得:
$4+16\overrightarrow{OA}•\overrightarrow{OC}+16=9$;
∴$\overrightarrow{OA}•\overrightarrow{OC}=-\frac{11}{16}$;
∴$(\overrightarrow{AC})^{2}=(\overrightarrow{OC}-\overrightarrow{OA})^{2}$
=${\overrightarrow{OC}}^{2}-2\overrightarrow{OA}•\overrightarrow{OC}+{\overrightarrow{OA}}^{2}$
=$1+\frac{22}{16}+1$
=$\frac{54}{16}$;
∴$|\overrightarrow{AC}|=\frac{3\sqrt{6}}{4}$;
即$AC=\frac{3\sqrt{6}}{4}$.
故答案为:$\frac{3\sqrt{6}}{4}$.
点评 考查三角形外接圆的概念,向量的数乘运算,以及向量数量积的运算及计算公式,向量减法的几何意义,以及要求$|\overrightarrow{AC}|$而求${\overrightarrow{AC}}^{2}$的方法.

| A. | 10 | B. | -30 | C. | -15 | D. | 25 |
| A. | $\frac{9}{10}$ | B. | -$\frac{9}{10}$ | C. | -$\frac{4}{5}$ | D. | $\frac{4}{5}$ |
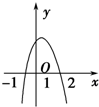
| A. | (-2,1) | B. | (0,3) | C. | (-1,2] | D. | (-∞,0)∪(3,+∞) |
| 组号 | 1 | 2 | 3 | 4 | 5 |
| 频数 | 28 | 32 | 28 | 32 | 30 |