题目内容
直线y=x+a与曲线y=a|x|有两个交点,则a的取值范围是( )A.a>0 B.a>1 C.0<a<1 D.0<a<1或a>1
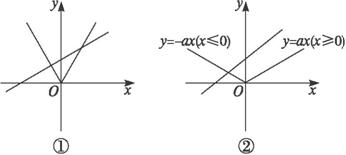
提示:直线y=x+a是斜率为1、纵截距为a的直线.曲线y=a|x|,当x≥0时,y=ax,这是一条斜率为a的射线;当x≤0时,y=-ax,是一条斜率为-a的射线.显然,当a>1时,y=x+a与y=-ax(x<0),y=ax(x>0)都相交,即直线y=x+a与y=a|x|有两个交点(如图①所示). 当0<a≤1时,y=x+a与射线y=-ax(x≤0)相交,而与射线y=ax(x≥0)不相交,故直线y=x+a与曲线y=a|x|只有一个交点(如图②所示). 答案:B
 练习册系列答案
练习册系列答案
本土教辅名校学案初中生辅导系列答案
轻巧夺冠青岛专用系列答案
名题文化步步高书系名题系列答案
倍速训练法一练通系列答案
金牌教辅夺冠金卷系列答案
海淀名师名校百分卷系列答案
8848高中同步学情跟进卷系列答案
中考实战名校在招手系列答案

伴你学山西系列答案
相关题目
已知f(x)是定义在R上的且以2为周期的偶函数,当0≤x≤1时,f(x)=x2,如果直线y=x+a与曲线y=f(x)恰有两个不同的交点,则实数a的值为( )
| A、2k(k∈Z) | ||
B、2k或2k+
| ||
| C、0 | ||
D、2k或2k-
|