题目内容
(本小题满分12分)
已知:如图,在四棱锥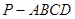 中,四边形
中,四边形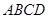 为正方形,
为正方形,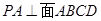 ,且
,且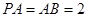 ,
,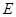 为
为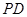 中点.
中点.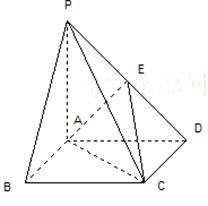
(1)证明: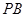 //平面
//平面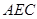 ;
;
(2)证明:平面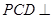 平面
平面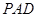 ;
;
(3)求二面角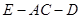 的正弦值.
的正弦值.
(1) 结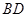 交
交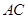 于点
于点 ,连结
,连结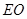 ,那么根据中位线性质可知
,那么根据中位线性质可知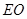 //
//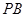 ,那么结合线面平行的判定定理来得到。
,那么结合线面平行的判定定理来得到。
(2)建立空间直角坐标系,然后结合空间向量的平面的法向量,借助于法向量的垂直来证明面面垂直。
(3)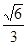
解析试题分析:解:(1)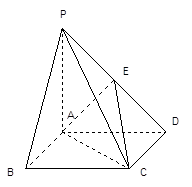
证明:连结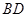 交
交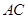 于点
于点 ,连结
,连结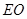 ……………………1分
……………………1分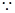
 为
为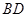 中点,
中点,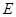 为
为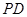 中点,
中点,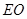 //
//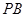 ……………………2分
……………………2分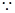
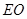
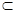 平面
平面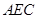 ,
,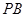
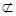 平面
平面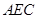 , ………3分
, ………3分
∴ 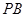 //平面
//平面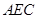 .
.
(2)证明: 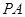 ⊥平面
⊥平面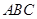
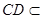 平面
平面 ,
,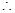
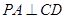 . …………4分
. …………4分
又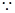 在正方形
在正方形 中
中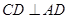 且
且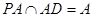 , …5分
, …5分
∴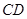
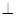 平面
平面 . ……………………6分
. ……………………6分
又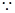
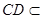 平面
平面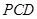 ,
,
∴平面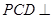 平面
平面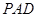 . ……………………7分
. ……………………7分
(3)如图,以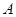 为坐标原点,
为坐标原点,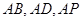 所在直线分别为
所在直线分别为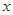 轴,
轴, 轴,
轴,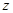 轴建立空
轴建立空
间直角坐标系. 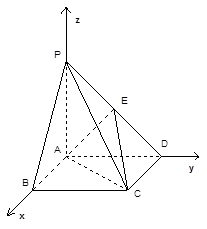
由 可知
可知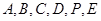 的坐标分别为
的坐标分别为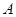 (0, 0, 0),
(0, 0, 0),  (2, 0, 0),
(2, 0, 0), (2, 2, 0),
(2, 2, 0),  (0, 2, 0),
(0, 2, 0),  (0, 0, 2),
(0, 0, 2), 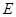 (0, 1, 1) .………9分
(0, 1, 1) .………9分
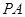
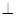 平面
平面 ,∴
,∴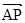 是平面
是平面 的法向量,
的法向量,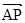 =(0, 0, 2).
=(0, 0, 2).
设平面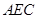 的法向量为
的法向量为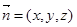

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 中,平面
中,平面 平面
平面 ,
,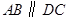 ,
,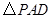 是等边三角形,已知
是等边三角形,已知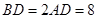 ,
,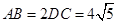 .
.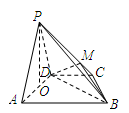
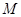 是
是 上的一点,证明:平面
上的一点,证明:平面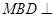 平面
平面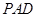 ;
;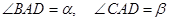 ,
,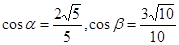 .
.
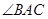 的大小;
的大小;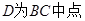 时,判断
时,判断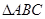 的形状,并求
的形状,并求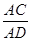 的值.
的值. 中,平面
中,平面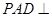 平面
平面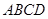 ,
,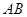 ∥
∥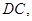
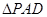 是正三角形,已知
是正三角形,已知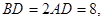
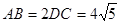
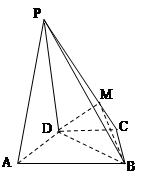
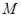 是
是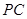 上的一点,求证:平面
上的一点,求证:平面 平面
平面 ;
;
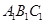 中,
中,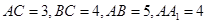 ,点
,点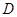 是
是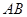 的中点.
的中点. 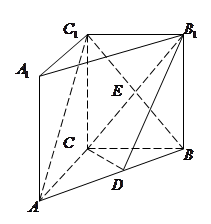
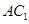 ∥平面
∥平面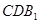 ;
;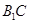 所成的角的余弦值;
所成的角的余弦值;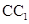 与平面
与平面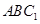 所成角的正弦值;
所成角的正弦值;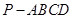 中,
中,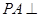 底面
底面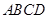 ,
,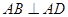 ,
, ,
,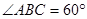 ,
,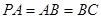 ,
, 是
是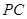 的中点。
的中点。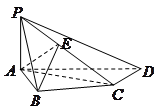
 ;
;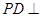 平面
平面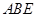 ;
;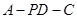 的正切值.
的正切值. 的底面
的底面 为菱 形 ,AC∩BD=O侧棱
为菱 形 ,AC∩BD=O侧棱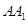 ⊥BD,点F为
⊥BD,点F为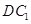 的中点.
的中点.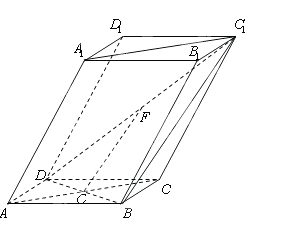
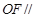 平面
平面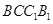 ;
;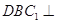 平面
平面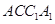 .
. 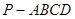 中,底面ABCD是边长为a的正方形,侧面
中,底面ABCD是边长为a的正方形,侧面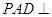 底面ABCD,且
底面ABCD,且 ,若E,F分别为PC,BD的中点.
,若E,F分别为PC,BD的中点.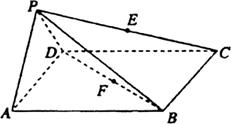
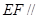 平面PAD;
平面PAD;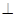 平面PAD;
平面PAD;  是正三角形,
是正三角形,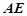 和
和 都垂直于平面
都垂直于平面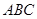 ,且
,且 ,
,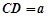 ,
,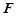 是
是 的中点.
的中点.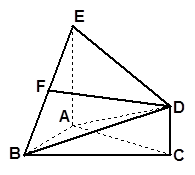
 ∥平面
∥平面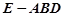 的体积.
的体积.