题目内容
(本小题满分12分)
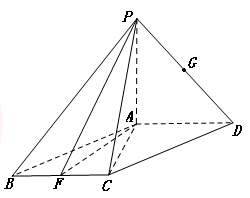
如图,在四棱锥 中,平面
中,平面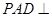 平面
平面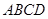 ,
,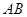 ∥
∥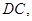
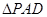 是正三角形,已知
是正三角形,已知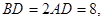
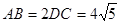
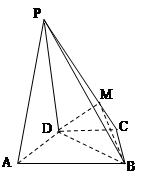
(1) 设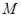 是
是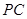 上的一点,求证:平面
上的一点,求证:平面 平面
平面 ;
;
(2) 求四棱锥 的体积.
的体积.
(1)关键证明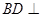 平面
平面 (2)
(2) 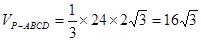
解析试题分析:(1)证明:在△ABD中,AD=4,BD=8,AB=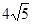
 故
故 ………2分
………2分
又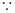 平面
平面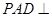 平面
平面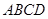 ,平面
,平面 ∩平面
∩平面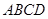 =AD,
=AD, 平面
平面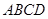
∴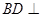 平面
平面 ………4分
………4分
又 平面MBD ∴平面
平面MBD ∴平面 平面
平面 ………5分
………5分
(2)解:过P作 交AD于O,
交AD于O,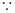 平面
平面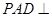 平面
平面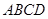 ∴
∴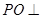 平面
平面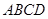
∴PO为四棱锥 的高,且PO=2
的高,且PO=2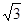 ………8分
………8分
又四边形ABCD是梯形,且Rt△ADB斜边AB上的高为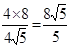 即为梯形ABCD的高 ∴梯形ABCD的面积为
即为梯形ABCD的高 ∴梯形ABCD的面积为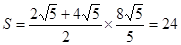 ………10分
………10分
故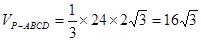 ………12分
………12分
考点:两平面垂直的判定定理;锥体的体积公式。
点评:证明直线与平面垂直、两平面垂直和直线与平面平行是常考知识点。对于求几何体的体积或表面积也是出题者经常考虑的。

练习册系列答案
相关题目
 平面ABCD,EF∥AB, AB=2EF=2AD=4,
平面ABCD,EF∥AB, AB=2EF=2AD=4,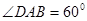 .
.
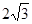 , BC=6.
, BC=6.
 ABC=60
ABC=60 ,EC
,EC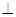 面ABCD,FA
面ABCD,FA
 中,底面
中,底面 是边长为2的菱形,
是边长为2的菱形, 是棱
是棱 上的动点.
上的动点.
 是
是 //平面
//平面 ;
; ,求证:
,求证: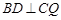 ;
;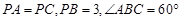 ,求四棱锥
,求四棱锥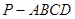 中,四边形
中,四边形 为正方形,
为正方形,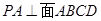 ,且
,且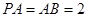 ,
,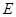 为
为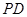 中点.
中点.
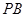 //平面
//平面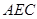 ;
;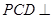 平面
平面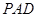 ;
;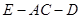 的正弦值.
的正弦值.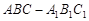 中,
中,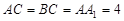 ,
, 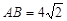 ,若
,若 是
是 中点.
中点. ∥平面
∥平面 ;
; 所成的角.
所成的角.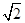 ,F是BC的中点.
,F是BC的中点.