题目内容
2.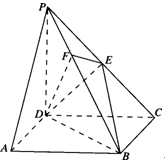 如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点,作EF⊥PB交PB于点F.
如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点,作EF⊥PB交PB于点F.证明:(1)PA∥平面EDB;
(2)PB⊥平面EFD;
(3)点F到平面BDE的距离.
分析 (1)由题意连接AC,AC交BD于O,连接EO,则EO是中位线,证出PA∥EO,由线面平行的判定定理知PA∥平面EDB;
(2)由PD⊥底面ABCD得PD⊥DC,再由DC⊥BC证出BC⊥平面PDC,即得BC⊥DE,再由ABCD是正方形证出DE⊥平面PBC,则有DE⊥PB,再由条件证出PB⊥平面EFD;
(3)通过求解三角形可得BE、BF、EF的长度,然后利用等积法求点F到平面BDE的距离.
解答 (1)证明:连接AC,AC交BD于O,连接EO.
∵底面ABCD是正方形,∴点O是AC的中点.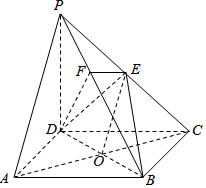
∴在△PAC中,EO是中位线,得PA∥EO,
∵EO?平面EDB,且PA?平面EDB,
∴PA∥平面EDB;
(2)证明:∵PD⊥底面ABCD,且DC?底面ABCD,∴PD⊥BC.
∵底面ABCD是正方形,∴DC⊥BC,
∴BC⊥平面PDC.
∵DE?平面PDC,∴BC⊥DE.
又∵PD=DC,E是PC的中点,∴DE⊥PC,则DE⊥平面PBC.
∵PB?平面PBC,∴DE⊥PB.
又∵EF⊥PB,且DE∩EF=E,
∴PB⊥平面EFD;
(3)∵PD=DC=2,PC=2$\sqrt{2}$,PB=2$\sqrt{3}$,PE=$\sqrt{2}$,
∵$\frac{EF}{PE}=\frac{BC}{PB}$,∴EF=$\frac{\sqrt{6}}{3}$,PF=$\frac{2\sqrt{3}}{3}$,FB=2$\sqrt{3}$-$\frac{2\sqrt{3}}{3}=\frac{4\sqrt{3}}{3}$,
DE=$\sqrt{2}$,BD=2$\sqrt{2}$,BE=$\sqrt{D{B}^{2}-D{E}^{2}}=\sqrt{6}$.
设点F到平面BDE的距离为h,
由VB-EFD=VD-BEF,得$\frac{1}{3}×\frac{1}{2}×DE×EF×BF=\frac{1}{3}×\frac{1}{2}×DE×BE×h$,
∴h=$\frac{EF×BF}{BE}$=$\frac{\frac{\sqrt{6}}{3}×\frac{4\sqrt{3}}{3}}{\sqrt{6}}=\frac{4\sqrt{3}}{9}$.
点评 本题主要考查线面平行和线面垂直的判定,要求熟练掌握相应的判定定理,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{9}{7}$ | B. | 3 | C. | $\frac{3}{4}$ | D. | $\frac{7}{9}$ |
| A. | $\sqrt{33}$ | B. | $\sqrt{17}$ | C. | $\sqrt{41}$ | D. | $\sqrt{42}$ |
| A. | 2i | B. | -2i | C. | 2+2i | D. | 2-2i |
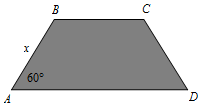 无锡市要建造一条防洪堤,其横断面为等腰梯形,腰与底边成角为60°(如图),考虑到防洪堤坚固性及石块用料等因素,设计基横断面要求面积为$6\sqrt{3}$平方米,且高度不低于$\sqrt{3}$米,记防洪堤横断面的腰长为x(米),外周长(梯形的上底线段BC与两腰长的和)为y(米).
无锡市要建造一条防洪堤,其横断面为等腰梯形,腰与底边成角为60°(如图),考虑到防洪堤坚固性及石块用料等因素,设计基横断面要求面积为$6\sqrt{3}$平方米,且高度不低于$\sqrt{3}$米,记防洪堤横断面的腰长为x(米),外周长(梯形的上底线段BC与两腰长的和)为y(米).