题目内容
设数列{an}的前n项和为Sn,a1=1,且数列{Sn}是以2为公比的等比数列.
(1)求数列{an}的通项公式;
(2)求a1+a3+…+a2n+1.
解析 (1)∵S1=a1=1,且数列{Sn}是以2为公比的等比数列,∴Sn=2n-1,
又当n≥2时,an=Sn-Sn-1=2n-2(2-1)=2n-2.
∴an=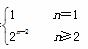
(2)a3,a5,…,a2n+1是以2为首项,以4为公比的等比数列,
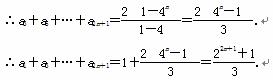 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
设数列{an}的前n项和为Sn,a1=1,且数列{Sn}是以2为公比的等比数列.
(1)求数列{an}的通项公式;
(2)求a1+a3+…+a2n+1.
解析 (1)∵S1=a1=1,且数列{Sn}是以2为公比的等比数列,∴Sn=2n-1,
又当n≥2时,an=Sn-Sn-1=2n-2(2-1)=2n-2.
∴an=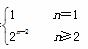
(2)a3,a5,…,a2n+1是以2为首项,以4为公比的等比数列,
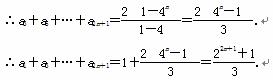 .
.

 阅读快车系列答案
阅读快车系列答案