题目内容
已知数列 中,
中, ,对于
,对于 ,以
,以 为系数的一元二次方程
为系数的一元二次方程
 都有实数根
都有实数根 ,且满足
,且满足 .
.
(Ⅰ)求证:数列 是等比数列;
是等比数列;
(Ⅱ)求数列 的通项公式; (Ⅲ)求
的通项公式; (Ⅲ)求 的前
的前 项和
项和 .
.
(Ⅰ) 解:∵ ,∴
,∴ ,又∵
,又∵ ,∴
,∴ ,
,
∴ ,
,
∴椭圆的标准方程为 .
.
(Ⅱ)证:当 的斜率为0时,显然
的斜率为0时,显然 ,满足题意,
,满足题意,
当 的斜率不为0时,设
的斜率不为0时,设 方程为
方程为 ,
,
代入椭圆方程整理得: .
.
 ,
, ,
, .
.
则

 ,
,
而
∴ ,从而
,从而 .
.
综合可知:对于任意的割线 ,恒有
,恒有 .
.
(Ⅲ)解: ,
,
即: ,
,
当且仅当 ,即
,即 (此时适合于
(此时适合于 的条件)取到等号.
的条件)取到等号.
∴△ABF面积的最大值是 .
.

练习册系列答案
相关题目
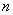 为奇数,则
为奇数,则 被9除得的余数是…( )
被9除得的余数是…( ) ,则称数列
,则称数列 为“调和数列”.已知正项数列
为“调和数列”.已知正项数列 为“调和数列”,且
为“调和数列”,且 ,则
,则 的最大值是( )
的最大值是( ) ,
, ,
, ,
, ,
, ,
, .
. 中,角
中,角 所对的边分别为
所对的边分别为 ,若
,若 ,b=
,b= ,
, ,则
,则 ( )
( ) B.
B. C.
C.
 ,则
,则 =______________
=______________ 中,
中, 中点为
中点为 ,若
,若 到各边的距离都相等,则
到各边的距离都相等,则 ”.若把该结论推广到空间,则有结论:“在棱长都相等的四面体
”.若把该结论推广到空间,则有结论:“在棱长都相等的四面体 中,若
中,若 的中心为
的中心为 ,四面体内部一点
,四面体内部一点 到四面体各面的距离都相等,
到四面体各面的距离都相等, ( )
( ) ,
, ”是全称命题;
”是全称命题; ”的否定是“
”的否定是“ ,使
,使 ”;
”; ,则
,则 ;
;  为假命题,则
为假命题,则 、
、 均为假命题.
均为假命题.