题目内容
设U=R,集合A={x|x2+3x+2=0},B={x|x2+(m+1)x+m=0}.若(∁UA)∩B=∅,试求m的值.
解:易知A={-2,-1}.
由(∁UA)∩B=∅,得B⊆A,
∵方程x2+(m+1)x+m=0的判别式Δ=(m+1)2-4m=(m-1)2≥0,∴B≠∅.
∴B={-1}或B={-2}或B={-1,-2}.
①若B={-1},则m=1;
②若B={-2},则应有-(m+1)=(-2)+(-2)=-4,且m=(-2)×(-2)=4,这两式不能同时成立,∴B≠{-2}.
③若B={-1,-2},则应有-(m+1)=(-1)+(-2)=-3,且m=(-1)×(-2)=2,由这两式得m=2.经检验知m=1和m=2符合条件.∴m=1或2.

练习册系列答案
相关题目
 <
< D.
D. <
<
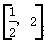 时,函数f(x)=x+
时,函数f(x)=x+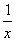 >
>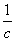 恒成立.如果p或q为真命题,p且q为假命题,求c的取值范围.
恒成立.如果p或q为真命题,p且q为假命题,求c的取值范围.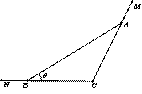 已知
已知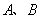 分别在射线
分别在射线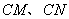 (不含端点
(不含端点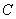 )上运动,
)上运动,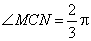 ,在
,在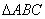 中,角
中,角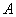 、
、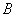 、
、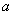 、
、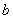 、
、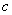 .
.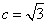 ,
,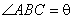 ,试用
,试用 表示
表示