题目内容
18.设n∈N*,则$\sqrt{\underbrace{11…1}_{2n个}-\underbrace{22…2}_{n个}}$=( )| A. | $\underbrace{33…3}_{n个}$ | B. | $\underbrace{33…3}_{2n-1个}$ | C. | $\underbrace{33…3}_{{2^n}-1个}$ | D. | $\underbrace{33…3}_{2n个}$ |
分析 利用数列知识,即可求解.
解答 解:$\sqrt{\underbrace{11…1}_{2n个}-\underbrace{22…2}_{n个}}=\sqrt{\frac{{{{10}^{2n}}-1}}{9}-\frac{{2({{10}^n}-1)}}{9}}=\sqrt{\frac{{{{({{10}^n}-1)}^2}}}{9}}=\frac{{{{10}^n}-1}}{3}$=$\underbrace{33…3}_{n个}$.
故选A.
点评 本题主要考查推理证明的相关知识,比较基础.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
3.某手机厂商推出一款6寸大屏手机,现对500名该手机用户(200名女性,300名男性)进行调查,对手机进行评分,评分的频数分布表如下:
(1)完成下列频率分布直方图,并指出女性用户和男性用户哪组评分更稳定(不计算具体值,给出结论即可);
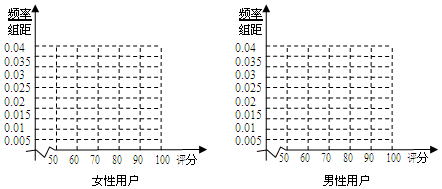
(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意抽取3名用户,求3名用户中评分小于90分的人数的分布列和期望.
| 女性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 20 | 40 | 80 | 50 | 10 | |
| 男性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 45 | 75 | 90 | 60 | 30 |

(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意抽取3名用户,求3名用户中评分小于90分的人数的分布列和期望.
10.函数y=$\frac{e^x}{x}$的大致图象是( )
| A. |  | B. |  | C. |  | D. |  |
15.如果关于x的不等式(a2-4)x2+(a+2)x-1≥0的解集是空集,则实数a的取值范围是( )
| A. | $-2≤a<\frac{6}{5}$ | B. | $-2≤a≤\frac{5}{6}$ | C. | -2≤a<1 | D. | -2≤a≤1 |