题目内容
8.某几何体的三视图如图所示,则该几何体的表面积为$10+2\sqrt{5}+6\sqrt{2}$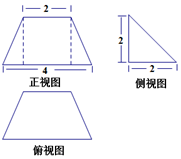
分析 几何体的直观图是四面体,求出每个面的面积,即可得出结论.
解答  解:几何体的直观图是四面体,每个面的面积分别为
解:几何体的直观图是四面体,每个面的面积分别为
$\frac{1}{2}×(2+4)×2$+2×2+$\frac{1}{2}×2×\sqrt{5}×2$+$\frac{1}{2}(2+4)×2\sqrt{2}$
=$10+2\sqrt{5}+6\sqrt{2}$,
故答案为$10+2\sqrt{5}+6\sqrt{2}$.
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
相关题目
3.已知双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的右焦点为F,过F作双曲线C渐近线的垂线,垂足为A,且交y轴于B,若$\overrightarrow{BA}=2\overrightarrow{AF}$,则双曲线的离心率为( )
| A. | $\frac{{\sqrt{6}}}{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{6}}}{2}$ |
20.已知奇函数f(x)在[0,+∞)上是增函数,若f(lnx)<0,则( )
| A. | $\frac{1}{e}$<x<1或x>1 | B. | 1<x<e | C. | 0<x<e或x>e | D. | 0<x<1 |
18.设n∈N*,则$\sqrt{\underbrace{11…1}_{2n个}-\underbrace{22…2}_{n个}}$=( )
| A. | $\underbrace{33…3}_{n个}$ | B. | $\underbrace{33…3}_{2n-1个}$ | C. | $\underbrace{33…3}_{{2^n}-1个}$ | D. | $\underbrace{33…3}_{2n个}$ |





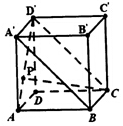
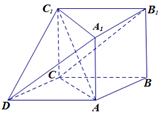 如图所示三棱柱ABC-A1B1C1中,AA1⊥平面ABC,四边形ABCD为平行四边形,AD=2CD,AC⊥CD.
如图所示三棱柱ABC-A1B1C1中,AA1⊥平面ABC,四边形ABCD为平行四边形,AD=2CD,AC⊥CD.