题目内容
1.2016年上半年,股票投资人袁先生同时投资了甲、乙两只股票,其中甲股票赚钱的概率为$\frac{1}{3}$,赔钱的概率是$\frac{2}{3}$;乙股票赚钱的概率为$\frac{1}{4}$,赔钱的概率为$\frac{3}{4}$.对于甲股票,若赚钱则会赚取5万元,若赔钱则损失4万元;对于乙股票,若赚钱则会赚取6万元,若赔钱则损失5万元.(Ⅰ)求袁先生2016年上半年同时投资甲、乙两只股票赚钱的概率;
(Ⅱ)试求袁先生2016年上半年同事投资甲、乙两只股票的总收益的分布列和数学期望.
分析 (Ⅰ)利用互斥事件概率加法公式和相互独立事件概率乘法公式能求出袁先生2016年上半年同时投资甲、乙两只股票赚钱的概率.
(Ⅱ)用X万元表示袁先生2016年上半年同时投资甲、乙两只股票的总收益,则X所有可能取值为-9,0,2,11,分别求出相应的概率,由此能求出X的分布列和数学期望.
解答 解:(Ⅰ)袁先生2016年上半年同时投资甲、乙两只股票赚钱的概率为:
p=$\frac{1}{3}×\frac{1}{4}+\frac{2}{3}×\frac{1}{4}$=$\frac{1}{4}$.
(Ⅱ)用X万元表示袁先生2016年上半年同时投资甲、乙两只股票的总收益,
则X所有可能取值为-9,0,2,11,
P(X=-9)=$\frac{2}{3}×\frac{3}{4}$=$\frac{1}{2}$,
P(X=0)=$\frac{1}{3}×\frac{3}{4}$=$\frac{1}{4}$,
P(X=2)=$\frac{2}{3}×\frac{1}{4}$=$\frac{1}{6}$,
P(X=11)=$\frac{1}{3}×\frac{1}{4}$=$\frac{1}{12}$,
∴X的分布列为:
| X | -9 | 0 | 2 | 11 |
| P | $\frac{1}{2}$ | $\frac{1}{4}$ | $\frac{1}{6}$ | $\frac{1}{12}$ |
点评 本题考查概率的求示,考查离散型随机变量的分布列及期望的求法,是中档题,解题时要认真审题,注意相互独立事件同时发生的概率,

练习册系列答案
相关题目
6.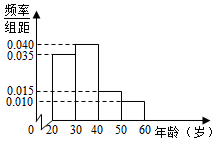 某学校有120名教师,且年龄都在20岁到60岁之间,各年龄段人数按分组,其频率分布直方图如图所示,学校要求每名教师都要参加两项培训,培训结束后进行结业考试.已知各年龄段两项培训结业考试成绩优秀的人数如表示,假设两项培训是相互独立的,结业考试成绩也互不影响.
某学校有120名教师,且年龄都在20岁到60岁之间,各年龄段人数按分组,其频率分布直方图如图所示,学校要求每名教师都要参加两项培训,培训结束后进行结业考试.已知各年龄段两项培训结业考试成绩优秀的人数如表示,假设两项培训是相互独立的,结业考试成绩也互不影响.
(1)若用分层抽样法从全校教师中抽取一个容量为40的样本,求从年龄段[20,30)抽取的人数;
(2)求全校教师的平均年龄;
(3)随机从年龄段[20,30)和[30,40)内各抽取1人,设这两人中两项培训结业考试成绩都优秀的人数为X,求X的概率分布和数学期望.
 某学校有120名教师,且年龄都在20岁到60岁之间,各年龄段人数按分组,其频率分布直方图如图所示,学校要求每名教师都要参加两项培训,培训结束后进行结业考试.已知各年龄段两项培训结业考试成绩优秀的人数如表示,假设两项培训是相互独立的,结业考试成绩也互不影响.
某学校有120名教师,且年龄都在20岁到60岁之间,各年龄段人数按分组,其频率分布直方图如图所示,学校要求每名教师都要参加两项培训,培训结束后进行结业考试.已知各年龄段两项培训结业考试成绩优秀的人数如表示,假设两项培训是相互独立的,结业考试成绩也互不影响.| 年龄分组 | A项培训成绩优秀人数 | B项培训成绩优秀人数 |
| [20,30) | 30 | 18 |
| [30,40) | 36 | 24 |
| [40,50) | 12 | 9 |
| [50,60] | 4 | 3 |
(2)求全校教师的平均年龄;
(3)随机从年龄段[20,30)和[30,40)内各抽取1人,设这两人中两项培训结业考试成绩都优秀的人数为X,求X的概率分布和数学期望.
10.设A,B,C,D是平面上互异的四个点,若($\overrightarrow{DB}$+$\overrightarrow{DC}$-2$\overrightarrow{DA}$)•($\overrightarrow{AB}$-$\overrightarrow{AC}$)=0,则△ABC的形状是( )
| A. | 直角三角形 | B. | 等腰三角形 | C. | 锐角三角形 | D. | 钝角三角形 |
11.2015年12月27日全国人大常委会表决通过了人口与计划生育法修正案全面二孩定于20I6年1月1日起正式实施,为了解适龄民众对放开生育二胎政策的态度,某机构从某市选取70后和80后作为调查对象.随机调查了100位,得到数据如下表:
(1)以这100个人的样本数据估计该市的总体数据,且以频率估计概率,若以该市70后公民中随机抽取3位,记其中生二孩的人数为X,求随机变量X的分布列和数学期望.
(2)根据调查数据,是否在犯错误的概率不超过0.1的前提下(有90%以上自把握)认为“生二孩与年龄有关”?并说明理由.
| 生二孩 | 不生二孩 | 合计 | |
| 70后 | 30 | 15 | 45 |
| 80后 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
(2)根据调查数据,是否在犯错误的概率不超过0.1的前提下(有90%以上自把握)认为“生二孩与年龄有关”?并说明理由.