题目内容
8.在△ABC中,内角A,B,C所对的边分别为a,b,c,若(a+b-c)(a-b+c)=bc.(Ⅰ)求A的值;
(Ⅱ)已知向量$\overrightarrow{m}$=$(c,\sqrt{3}+1)$,$\overrightarrow{n}$=(b,2),若$\overrightarrow{m}$与$\overrightarrow{n}$共线,求tanC.
分析 (Ⅰ)整理已知等式可得b2+c2-a2=bc,利用余弦定理可得$cosA=\frac{1}{2}$,结合范围0<A<π,即可解得A的值.
(Ⅱ)由m与n共线可得$2c=(\sqrt{3}+1)b$,由正弦定理可得$2sinC=(\sqrt{3}+1)sinB$,结合sinB=sin(A+C),由三角函数恒等变换的应用即可求值.
解答 (本题满分为12分)
解:(Ⅰ)∵(a+b-c)(a-b+c)=bc,
∴a2-b2-c2+2bc=bc,
∴b2+c2-a2=bc…(3分)
由余弦定理知:∵b2+c2-a2=2bccosA,…(5分)
∴$cosA=\frac{1}{2}$,
∵0<A<π,
∴$A=\frac{π}{3}$…(6分)
(Ⅱ)∵m与n共线∴$2c=(\sqrt{3}+1)b$,…(7分)
由正弦定理知:$2sinC=(\sqrt{3}+1)sinB$,…(8分)
又∵在△ABC中,sinB=sin(A+C),
∴$2sinC=(\sqrt{3}+1)sin(\frac{π}{3}+C)$,…(10分)
即:$2sinC=(\sqrt{3}+1)(\frac{{\sqrt{3}}}{2}cosC+\frac{1}{2}sinC)$$(3-\sqrt{3})sinC=(\sqrt{3}+3)cosC$,
∴$tanC=2+\sqrt{3}$…(12分)
点评 本题主要考查了平面向量数量积的运算,正弦定理,余弦定理,三角函数恒等变换的应用在解三角形中的应用,考查了转化思想,属于中档题.

练习册系列答案
相关题目
18.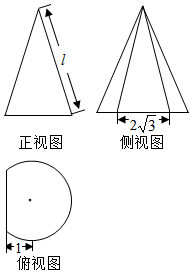 如图所示是沿圆锥的两条母线将圆锥削去一部分后所得几何体的三视图,其体积为$\frac{16π}{9}+\frac{{2\sqrt{3}}}{3}$,则圆锥的母线长为( )
如图所示是沿圆锥的两条母线将圆锥削去一部分后所得几何体的三视图,其体积为$\frac{16π}{9}+\frac{{2\sqrt{3}}}{3}$,则圆锥的母线长为( )
 如图所示是沿圆锥的两条母线将圆锥削去一部分后所得几何体的三视图,其体积为$\frac{16π}{9}+\frac{{2\sqrt{3}}}{3}$,则圆锥的母线长为( )
如图所示是沿圆锥的两条母线将圆锥削去一部分后所得几何体的三视图,其体积为$\frac{16π}{9}+\frac{{2\sqrt{3}}}{3}$,则圆锥的母线长为( )| A. | $2\sqrt{2}$ | B. | $2\sqrt{3}$ | C. | 4 | D. | $\sqrt{2}+\sqrt{3}$ |
19.已知函数$f(x)=\left\{\begin{array}{l}{log_5}x,x>0\\{2^x}\;\;,x≤0\end{array}\right.$,则$f(f(\frac{1}{25}))$=( )
| A. | 4 | B. | $\frac{1}{4}$ | C. | -4 | D. | $-\frac{1}{4}$ |
13.设全集U={x∈N|x≥2},集合A={x|x2-5x≥0},B={x|x≥3},则(∁UA)∩B=( )
| A. | {3} | B. | {3.4} | C. | {3.4,5} | D. | {3.4,5,6} |
18.在等差数列{an}中,已知a4=2,a8=14,则a15等于( )
| A. | 32 | B. | -32 | C. | 35 | D. | -35 |