题目内容
7.若存在实数x,y满足$\left\{\begin{array}{l}{2x-y-2<0}\\{x-2y+2>0}\\{x+y-2>0}\\{m(x+1)-y=0}\\{\;}\end{array}\right.$,则实数m的取值范围是( )| A. | (0,$\frac{2}{7}$) | B. | ($\frac{2}{7}$,$\frac{2}{3}$) | C. | ($\frac{2}{3}$,$\frac{4}{5}$) | D. | ($\frac{2}{7}$,$\frac{4}{5}$) |
分析 作出平面区域,可得直线过定点D(-1,0),斜率为-m,结合图象可得m的不等式组,解不等式组可得.
解答 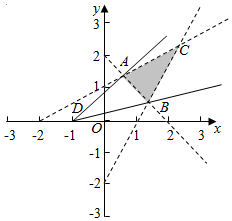 解:作出$\left\{\begin{array}{l}{2x-y-2<0}\\{x-2y+2>0}\\{x+y-2>0}\end{array}\right.$所对应的区域(如图△ABC即内部,不包括边界),
解:作出$\left\{\begin{array}{l}{2x-y-2<0}\\{x-2y+2>0}\\{x+y-2>0}\end{array}\right.$所对应的区域(如图△ABC即内部,不包括边界),
直线m(x+1)-y=0,可化为y=m(x+1),过定点D(-1,0),斜率为m,
存在实数x,y满足$\left\{\begin{array}{l}{2x-y-2<0}\\{x-2y+2>0}\\{x+y-2>0}\\{m(x+1)-y=0}\\{\;}\end{array}\right.$,
则直线需与区域有公共点,$\left\{\begin{array}{l}{x+y-2=0}\\{2x-y-2=0}\end{array}\right.$,
解得B($\frac{4}{3}$,$\frac{2}{3}$),$\left\{\begin{array}{l}{x+y-2=0}\\{x-2y+2=0}\end{array}\right.$,解得A($\frac{2}{3}$,$\frac{4}{3}$)
KDA=$\frac{\frac{4}{3}}{\frac{2}{3}+1}$=$\frac{4}{5}$,KDB=$\frac{\frac{2}{3}}{\frac{4}{3}+1}$=$\frac{2}{7}$,
∴$\frac{2}{7}$<m<$\frac{4}{5}$
故选:D.
点评 本题考查简单线性规划,准确作图是解决问题的关键,考查数形结合,转化思想的应用,属中档题.

练习册系列答案
相关题目
18.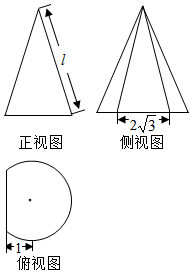 如图所示是沿圆锥的两条母线将圆锥削去一部分后所得几何体的三视图,其体积为$\frac{16π}{9}+\frac{{2\sqrt{3}}}{3}$,则圆锥的母线长为( )
如图所示是沿圆锥的两条母线将圆锥削去一部分后所得几何体的三视图,其体积为$\frac{16π}{9}+\frac{{2\sqrt{3}}}{3}$,则圆锥的母线长为( )
 如图所示是沿圆锥的两条母线将圆锥削去一部分后所得几何体的三视图,其体积为$\frac{16π}{9}+\frac{{2\sqrt{3}}}{3}$,则圆锥的母线长为( )
如图所示是沿圆锥的两条母线将圆锥削去一部分后所得几何体的三视图,其体积为$\frac{16π}{9}+\frac{{2\sqrt{3}}}{3}$,则圆锥的母线长为( )| A. | $2\sqrt{2}$ | B. | $2\sqrt{3}$ | C. | 4 | D. | $\sqrt{2}+\sqrt{3}$ |
12.设命题甲:关于x的式x2+2ax+1>0对一切x∈R恒成立,命题乙:对数函=log(4-2a)x在(0,+∞)上递减,那么甲是乙的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
19.已知函数$f(x)=\left\{\begin{array}{l}{log_5}x,x>0\\{2^x}\;\;,x≤0\end{array}\right.$,则$f(f(\frac{1}{25}))$=( )
| A. | 4 | B. | $\frac{1}{4}$ | C. | -4 | D. | $-\frac{1}{4}$ |