题目内容
已知
(1)判断 的奇偶性;
的奇偶性;
(2)讨论 的单调性;
的单调性;
(3)当 时,
时, 恒成立,求b的取值范围.
恒成立,求b的取值范围.
(1) 为奇函数;(2)
为奇函数;(2) 为增函数;(3)
为增函数;(3)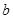 的取值范围是
的取值范围是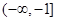 .
.
解析试题分析:(1)要判断 的单调性,首先考虑其定义域为
的单调性,首先考虑其定义域为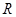 ,关于原点对称,又
,关于原点对称,又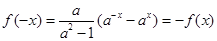 ,因此
,因此 为奇函数;(2)
为奇函数;(2) 的表达式中有
的表达式中有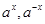 ,因此需要分
,因此需要分 和
和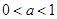 ,两种情况分类讨论,可以得到
,两种情况分类讨论,可以得到 在
在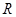 上单调递增;(3)根据题意,要使
上单调递增;(3)根据题意,要使 对任意
对任意 恒成立,只需
恒成立,只需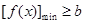 ,而由(2)
,而由(2) 在
在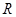 上单调递增,因此只需.
上单调递增,因此只需.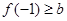 ,从而可以得到
,从而可以得到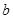 的取值范围为
的取值范围为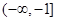 .
.
(1)函数定义域为R,关于原点对称,∵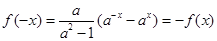 ,∴
,∴ 为奇函数; (2)当
为奇函数; (2)当 时,
时,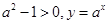 为增函数,
为增函数, 为减函数,
为减函数,
从而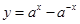 为增函数,∴
为增函数,∴ 为增函数.
为增函数.
当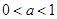 时,
时,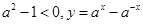 为减函数,∴
为减函数,∴ 为增函数,
为增函数,
故当 且
且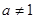 时,
时, 在
在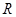 上单调递增;
上单调递增;
(3)由(2)知 在R上是增函数,∴在区间
在R上是增函数,∴在区间 上为增函数,
上为增函数,
∴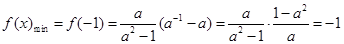 ,
,
∴要使 在
在 上恒成立,则
上恒成立,则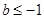 ,故
,故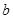 的取值范围是
的取值范围是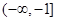 .
.
考点:1.函数奇偶性的判定;2.函数单调性判定;3.恒成立问题的处理方法.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
 是不全为
是不全为 的实数,函数
的实数,函数 ,
, ,方程
,方程 有实根,且
有实根,且 的根,反之,
的根,反之, 的值;(2)若
的值;(2)若 ,求
,求 的取值范围.
的取值范围. 为常数,
为常数, ,函数
,函数 ,
, 且方程
且方程 有等根.
有等根. 的解析式及值域;
的解析式及值域; ,
, ,若
,若 ,求实数
,求实数 的取值范围;
的取值范围;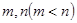 ,使
,使 的定义域和值域分别为
的定义域和值域分别为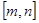 和
和 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.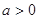 且
且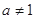 ,函数
,函数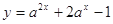 在
在 的最大值是14,求
的最大值是14,求 的值。
的值。
 的简图;
的简图; 有三个不等实根,求k值的集合;
有三个不等实根,求k值的集合; 时,函数
时,函数 的下方,试求出k值的集合。
的下方,试求出k值的集合。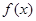 是定义在区间
是定义在区间 上的奇函数,且
上的奇函数,且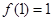 ,若
,若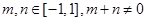 时,有
时,有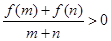 .
.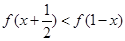 ;
;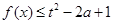 对
对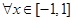 与
与 恒成立,求实数
恒成立,求实数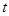 的取值范围.
的取值范围.
 在区间[0,3]上的最大值为2,则
在区间[0,3]上的最大值为2,则