题目内容
设函数
(1)画出 的简图;
的简图;
(2)若方程 有三个不等实根,求k值的集合;
有三个不等实根,求k值的集合;
(3)如果 时,函数
时,函数 的图象总在直线
的图象总在直线 的下方,试求出k值的集合。
的下方,试求出k值的集合。
(1)见解析;(2)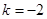 ;(3)
;(3)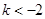 .
.
解析试题分析:(1)先去掉绝对值,将函数f(x)转化为分段函数,再分段画出函数的图象即可;因为g(x)的图象是一条过定点(7,0)直线的直线,找到直线与函数相切时k的值,且须满足切点 ;(3)
;(3) 的图象总在直线
的图象总在直线 的下方,即是求
的下方,即是求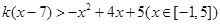 恒成立,解出不等式即得解.
恒成立,解出不等式即得解.
试题解析:(1)函数简图如下: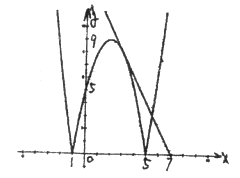
(2) 时,
时,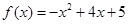 令
令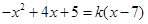 ,则
,则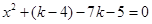
当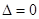 时,直线
时,直线 与抛物线
与抛物线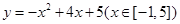 弧段相切,由
弧段相切,由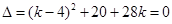 得:
得: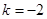 或
或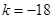 ,当
,当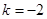 时,解之,得
时,解之,得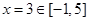 当
当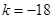 时,
时,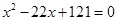 。解之,得
。解之,得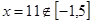 ,时直线
,时直线 与抛物线
与抛物线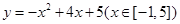 弧段相切于点(3,8),同时,直线
弧段相切于点(3,8),同时,直线 与抛物线
与抛物线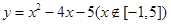 部分相交于不同两点。
部分相交于不同两点。
由图形可知,直线 绕点(7,0)转动时,除
绕点(7,0)转动时,除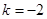 外的所有直线与图象无公共点或有两个公共点或有四个公共点。故
外的所有直线与图象无公共点或有两个公共点或有四个公共点。故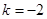 为所求;(3)设
为所求;(3)设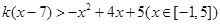 恒成立,
恒成立,
即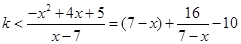 ,
,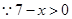 ,
,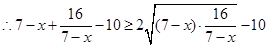
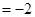
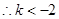 即为所求.
即为所求.
考点:1、二次函数的图象和性质;2、函数的零点.

练习册系列答案
相关题目
 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,若
,若 时,有
时,有

 对
对 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围 上的奇函数
上的奇函数 ,当
,当 时,
时,
 上单调递增,求实数
上单调递增,求实数 的取值范围。
的取值范围。
 的奇偶性;
的奇偶性; 时,
时, 恒成立,求b的取值范围.
恒成立,求b的取值范围. 为偶函数,曲线
为偶函数,曲线 过点
过点 ,
,  .
. 有斜率为0的切线,求实数
有斜率为0的切线,求实数 的取值范围;
的取值范围; 时函数
时函数 +1,h(x)=
+1,h(x)= ,x∈(-3,a],其中a为常数且a>0,令函数f(x)=g(x)·h(x).
,x∈(-3,a],其中a为常数且a>0,令函数f(x)=g(x)·h(x). 时,求函数f(x)的值域.
时,求函数f(x)的值域. +2.
+2.