题目内容
某工厂每天生产某种产品最多不超过40件，并且在生产过程中产品的正品率P与每日生产量
件间的关系为
，每生产一件正品盈利4000元，每出现一件次品亏损2000元．(注：正品率=产品中的正品件数÷产品总件数×100％)
(Ⅰ)将日利润
(元)表示成日产量
(件)的函数；
(Ⅱ)求该厂的日产量为多少件时，日利润最大?并求出日利润的最大值．
解：(Ⅰ)
．
∴所求的函数关系是
(Ⅱ)显然
.令
，解得
．
∴当
时，
；
当
时，
．
∴函数在
上是单调递增函数，
在
上是单调递减函数．
∴当时，函数取最大值，
最大值为
(元)．
∴该厂的日产量为30件时，日利润最大，其最大值为72000元．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
，每生产一件正品盈利4000元，每出现一件次品亏损2000元.（注：正品率=产品的正品件数÷产品总件数×100%）
，每生产一件正品盈利4000元，每出现一件次品亏损2000元.(注：正品率=产品的正品件数÷产品总件数×100%).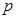
与每日生产产品件数
(
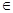
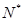)间的关系为
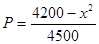，每生产一件正品盈利4000元，每出现一件次品亏损2000元.
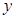（元）表示成日产量
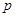与每日生产产品件数
(
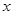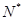)间的关系为
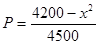，每生产一件正品盈利4000元，每出现一件次品亏损2000元.（注：正品率=产品的正品件数÷产品总件数×100%）
（元）表示成日产量