题目内容
某工厂每天生产某种产品最多不超过40件,并且在生产过程中产品的正品率P与每日和生产产品件数x(x∈N*)间的关系为P=| 4200-x2 | 4500 |
(Ⅰ)将日利润y(元)表示成日产量x(件)的函数;
(Ⅱ)求该厂的日产量为多少件时,日利润最大?并求出日利润的最大值.
分析:(1)根据题中正品率和盈利情况可得到关系式y=4000•
•x-2000(1-
)•x,整理后可得到答案.
(2)对(1)中函数进行求导数,令导函数等于0求出x的值,并求出y′>0、y′<0的x的范围,进而可得到答案.
| 4200-x2 |
| 4500 |
| 4200-x2 |
| 4500 |
(2)对(1)中函数进行求导数,令导函数等于0求出x的值,并求出y′>0、y′<0的x的范围,进而可得到答案.
解答:解:(1)y=4000•
•x-2000(1-
)•x=3600x-
x3
∴所求的函数关系是y=-
x3+3600x(x∈N*,1≤x≤40).
(Ⅱ)由上知,y′=3600-4x2,令y′=0,解得x=30.
∴当1≤x<30时,y′>0;当30<x≤40时,y′<0.
∴函数y=-
x3+3600x(x∈N*,1≤x≤40)在[1,30)上是单调递增函数,在(30,40]上是单调递减函数.
∴当x=30时,函数y-
x3+3600x(x∈N*,1≤x≤40)取最大值,最大值为-
×303+3600×30=72000(元).
∴该厂的日产量为30件时,日利润最大,其最大值为72000元
| 4200-x2 |
| 4500 |
| 4200-x2 |
| 4500 |
| 4 |
| 3 |
∴所求的函数关系是y=-
| 4 |
| 3 |
(Ⅱ)由上知,y′=3600-4x2,令y′=0,解得x=30.
∴当1≤x<30时,y′>0;当30<x≤40时,y′<0.
∴函数y=-
| 4 |
| 3 |
∴当x=30时,函数y-
| 4 |
| 3 |
| 4 |
| 3 |
∴该厂的日产量为30件时,日利润最大,其最大值为72000元
点评:本题主要考查根据已知条件列函数关系式、根据导数的正负判断函数的单调性问题.属基础题.

练习册系列答案
相关题目
 ,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%).
,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%).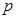 与每日生产产品件数
与每日生产产品件数 (
(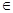
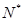 )间的关系为
)间的关系为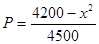 ,每生产一件正品盈利4000元,每出现一件次品亏损2000元.
,每生产一件正品盈利4000元,每出现一件次品亏损2000元.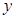 (元)表示成日产量
(元)表示成日产量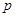 与每日生产产品件数
与每日生产产品件数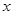 (
(
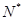 )间的关系为
)间的关系为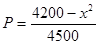 ,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%)
,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%) (元)表示成日产量
(元)表示成日产量