Question

(本小题满分12分) 某工厂每天生产某种产品最多不超过40件，并且在生产过程中产品的正品率P与每日生产产品件数x(x∈N^*)间的关系为P＝，每生产一件正品盈利4000元，每出现一件次品亏损2000元.(注：正品率=产品的正品件数÷产品总件数×100%).

(Ⅰ)将日利润y(元)表示成日产量x(件)的函数;

(Ⅱ)求该厂的日产量为多少件时，日利润最大？并求出日利润的最大值.

 

Answer 1

【答案】

（1）y=-+3600x(x∈N^*，1≤x≤40)（2）该厂的日产量为30件时，日利润最大，其最大值为7200元

【解析】

试题分析：解：(1)y＝4000··x-2000(1-)·x……………………………4分

=3600x-

∴所求的函数关系是y=-+3600x(x∈N^*，1≤x≤40). …………………………4分

(Ⅱ) 由函数y= （x>0）,y′＝3600-4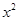，令y′＝0，解得x＝30.

∴当1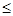x＜30时，y′＞0；当30＜x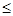40时，y′＜0.

∴函数y=在［1，30］上是单调递增函数，在[30，40］上是单调递减函数. ………………………………………………………………9分

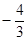∴当x=30时，函数y= (1≤x≤40)取最大值，最大值为×30³+3600×30＝7200(元).

∴该厂的日产量为30件时，日利润最大，其最大值为7200元 ……………………12分

考点：考查了函数的模型在实际中的运用。

点评：解决这类问题的关键是理解利润函数与成本和收入的关系式，同时要注意到函数的自编来那个的实际意义，得到定义域，结合函数 性质求解最值。属于中档题。