题目内容
7．函数f（x）=2-2sin2（$\frac{x}{2}$+π）的最小正周期是（ ）| A． | $\frac{π}{2}$ | B． | π | C． | 2π | D． | 4π |
分析 由条件利用三角恒等变换化简函数的解析式，再利用余弦函数的周期性得出结论．
解答 解：f（x）=2-2sin2（$\frac{x}{2}$+π）=2-2${sin}^{2}\frac{x}{2}$=2-2•$\frac{1-cosx}{2}$=1+cosx 的最小正周期为$\frac{2π}{1}$=2π，
故选：C．
点评 本题主要三角恒等变换，余弦函数的周期性，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
12．
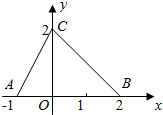如图，函数f（x）的图象为折线ACB，则不等式f（x）＞2x-1的解集是（ ）
如图，函数f（x）的图象为折线ACB，则不等式f（x）＞2x-1的解集是（ ）| A． | {x|-1＜x≤0} | B． | {x|-1≤x≤1} | C． | {x|-1≤x＜1} | D． | {x|-1＜x≤2} |