题目内容
.已知函数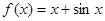
(Ⅰ)当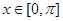 时,求
时,求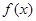 的值域
的值域
(Ⅱ)设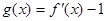 ,若
,若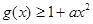 在
在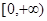 恒成立,求实数a的取值范围
恒成立,求实数a的取值范围
(III)设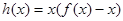 ,若
,若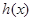 在
在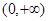 上的所有极值点按从小到大排成一列
上的所有极值点按从小到大排成一列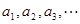 ,
,
求证: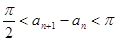
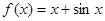
(Ⅰ)当
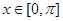 时,求
时,求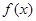 的值域
的值域(Ⅱ)设
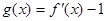 ,若
,若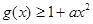 在
在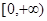 恒成立,求实数a的取值范围
恒成立,求实数a的取值范围(III)设
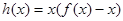 ,若
,若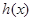 在
在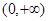 上的所有极值点按从小到大排成一列
上的所有极值点按从小到大排成一列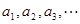 ,
,求证:
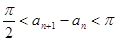
(Ⅰ)函数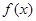 的值域为
的值域为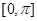 ;(Ⅱ)
;(Ⅱ) 的取值范围为
的取值范围为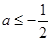 .(Ⅲ)
.(Ⅲ)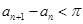 .
.
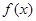 的值域为
的值域为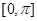 ;(Ⅱ)
;(Ⅱ) 的取值范围为
的取值范围为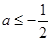 .(Ⅲ)
.(Ⅲ)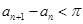 .
. 本试题主要是考查了导数在研究函数中的 运用。利用导数求解函数的单调区间,确定值域和运用不等式恒成立问题,得到参数的取值范围以及不等式的证明。
(1)因为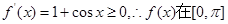 上单调递增.
上单调递增.
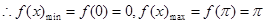 ,从而得到值域。
,从而得到值域。
(2)因为设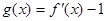 ,若
,若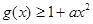 在
在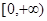 恒成立,可以构造函数
恒成立,可以构造函数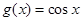 ,记
,记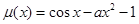 ,则
,则 .
.
利用导数的思想确定最值得到参数的范围。
(3)根据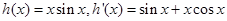
令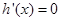 ,则
,则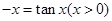 .
.
那么可知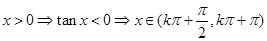 借助于正切函数的单调区间得到结论。
借助于正切函数的单调区间得到结论。
解:(Ⅰ)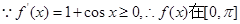 上单调递增.
上单调递增.
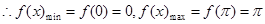
所以函数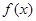 的值域为
的值域为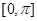 ……………………. 4分
……………………. 4分
(Ⅱ)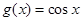 ,记
,记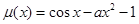 ,则
,则 .
.
当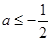 时,
时,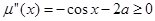 ,所以
,所以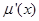 在
在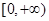 上单调递增.
上单调递增.
又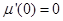 ,故
,故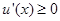 .从而
.从而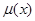 在
在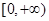 上单调递增.
上单调递增.
所以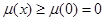 ,即
,即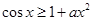 在
在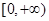 上恒成立………….7分
上恒成立………….7分
当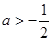 时,
时,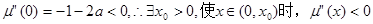 .
.
所以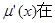
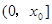 上单调递减,从而
上单调递减,从而 ,
,
故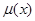 在
在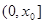 上单调递减,
上单调递减,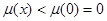 这与已知矛盾. …………….9分
这与已知矛盾. …………….9分
综上,故 的取值范围为
的取值范围为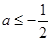 .
.
(Ⅲ)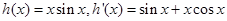
令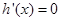 ,则
,则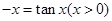 .
.
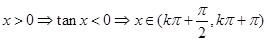
依题意可知 ,
,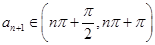
从而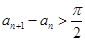 . …………………….12分
. …………………….12分
又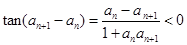 ,所以
,所以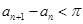 . …………….14分
. …………….14分
(1)因为
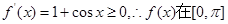 上单调递增.
上单调递增.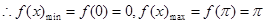 ,从而得到值域。
,从而得到值域。(2)因为设
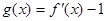 ,若
,若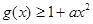 在
在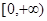 恒成立,可以构造函数
恒成立,可以构造函数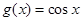 ,记
,记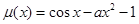 ,则
,则 .
.利用导数的思想确定最值得到参数的范围。
(3)根据
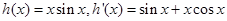
令
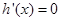 ,则
,则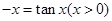 .
.那么可知
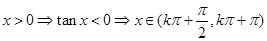 借助于正切函数的单调区间得到结论。
借助于正切函数的单调区间得到结论。解:(Ⅰ)
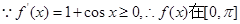 上单调递增.
上单调递增.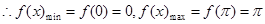
所以函数
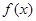 的值域为
的值域为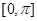 ……………………. 4分
……………………. 4分(Ⅱ)
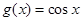 ,记
,记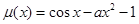 ,则
,则 .
.当
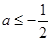 时,
时,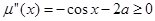 ,所以
,所以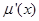 在
在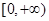 上单调递增.
上单调递增.又
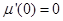 ,故
,故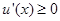 .从而
.从而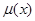 在
在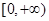 上单调递增.
上单调递增.所以
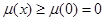 ,即
,即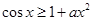 在
在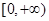 上恒成立………….7分
上恒成立………….7分当
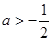 时,
时,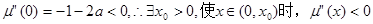 .
.所以
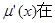
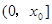 上单调递减,从而
上单调递减,从而 ,
, 故
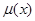 在
在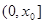 上单调递减,
上单调递减,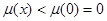 这与已知矛盾. …………….9分
这与已知矛盾. …………….9分综上,故
 的取值范围为
的取值范围为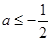 .
.(Ⅲ)
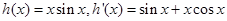
令
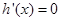 ,则
,则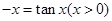 .
.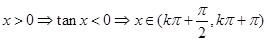
依题意可知
 ,
,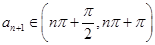
从而
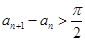 . …………………….12分
. …………………….12分又
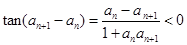 ,所以
,所以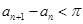 . …………….14分
. …………….14分
练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
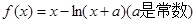 .
.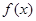 的单调区间;
的单调区间;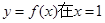 处取得极值时,若关于
处取得极值时,若关于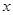 的方程
的方程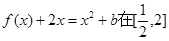 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数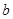 的取值范围;
的取值范围;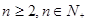 时,有
时,有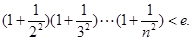
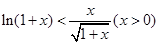
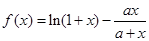 在
在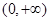 上单调递增,求实数
上单调递增,求实数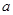 的取值范围.
的取值范围.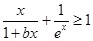 在
在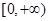 上恒成立,求实数
上恒成立,求实数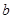 的最大值.
的最大值.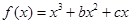 的导函数的图象关于直线x=2对称.
的导函数的图象关于直线x=2对称.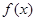 在
在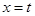 处取得极小值,记此极小值为
处取得极小值,记此极小值为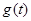 ,求
,求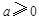 ,
,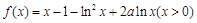 .
.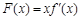 ,讨论
,讨论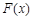 在
在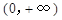 内的单调性并求极值;
内的单调性并求极值;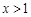 时,试判断
时,试判断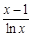 与
与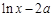 的大小.
的大小.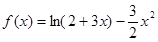 .
.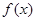 在[0,1]上的极值;
在[0,1]上的极值;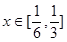 ,不等式
,不等式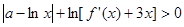 成立,求实数
成立,求实数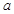 的取值范围;
的取值范围;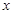 的方程
的方程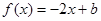 在[0,1]上恰有两个不同的实根,求实数
在[0,1]上恰有两个不同的实根,求实数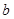 的取值范围.
的取值范围.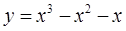 的单调递增区间为_______________
的单调递增区间为_______________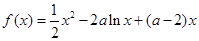 ,
,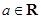 .
.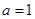 时,求函数
时,求函数 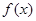 的最小值;
的最小值; 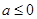 时,讨论函数
时,讨论函数 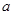 ,对任意的
,对任意的 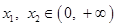 ,且
,且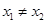 ,有
,有 ,恒成立,若存在求出
,恒成立,若存在求出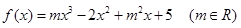 且
且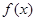 在
在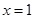 处取得极小值
处取得极小值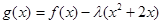 在
在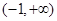 上是增函数,求实数
上是增函数,求实数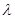 的取值范围。
的取值范围。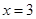 是函数
是函数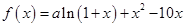 的一个极值点.
的一个极值点.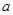 ;
;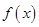 的单调区间;
的单调区间;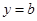 与函数
与函数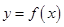 的图象有3个交点,求
的图象有3个交点,求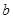 的取值范围.
的取值范围.