题目内容
3.若直线l的一个方向向量为$\overrightarrow{a}$=(2,5,7),平面α的一个法向量为$\overrightarrow{μ}$=(1,1,-1),则( )| A. | l∥α | B. | l⊥α | C. | l?α | D. | A、C都有可能 |
分析 利用向量的数量积判断直线与平面的位置关系即可.
解答 解:直线l的一个方向向量为$\overrightarrow{a}$=(2,5,7),平面α的一个法向量为$\overrightarrow{μ}$=(1,1,-1),
可得$\overrightarrow{a}$•$\overrightarrow{μ}$=(=(2,5,7)(1,1,-1)=2+5-7=0,
所以l∥α.或l?α.
故选:D.
点评 本题考查空间向量的数量积的应用,直线与平面垂直的判断,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.一个圆经过椭圆$\frac{{x}^{2}}{4}$+y2=1的三个顶点,且圆心在x轴的正半轴上,则该圆的标准方程为( )
| A. | (x-$\frac{3}{2}$)2+y2=$\frac{25}{4}$ | B. | (x+$\frac{3}{4}$)2+y2=$\frac{25}{16}$ | C. | (x-$\frac{3}{4}$)2+y2=$\frac{25}{16}$ | D. | (x-$\frac{3}{4}$)2+y2=$\frac{25}{4}$ |
14.已知tanθ=2,且θ∈$({0,\frac{π}{2}})$,则cos2θ=( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $-\frac{3}{5}$ | D. | $-\frac{4}{5}$ |
8.直线y=2b与双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左支、右支分别交于A、B两点,O为坐标原点,且△AOB为等腰直角三角形,则该双曲线的离心率为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{\sqrt{30}}{5}$ | D. | $\frac{3\sqrt{5}}{5}$ |
12.函数$y=\sqrt{x}-1$的值域是( )
| A. | [0,+∞) | B. | (0,+∞) | C. | [-1,+∞) | D. | (-1,+∞) |
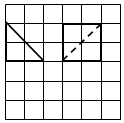 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的正视图(等腰直角三角形)和侧视图,且该几何体的体积为$\frac{8}{3}$,则该几何体的俯视图可以是( )
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的正视图(等腰直角三角形)和侧视图,且该几何体的体积为$\frac{8}{3}$,则该几何体的俯视图可以是( )

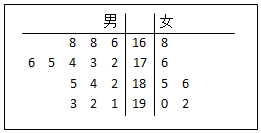 某公司从大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分).公司规定:成绩在180分以上者到甲部门工作,180分以下者到乙部门工作,另外只有成绩高于180分的男生才能担任助理工作.
某公司从大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分).公司规定:成绩在180分以上者到甲部门工作,180分以下者到乙部门工作,另外只有成绩高于180分的男生才能担任助理工作.