题目内容
20.已知双曲线$\frac{x^2}{m}-\frac{y^2}{8}=1$的离心率为$\sqrt{5}$,则实数m的值为2.分析 判断双曲线的m>0,求出a,b,c,由离心率公式e=$\frac{c}{a}$,建立方程,解方程可得m的值.
解答 解:双曲线$\frac{x^2}{m}-\frac{y^2}{8}=1$(m>0),
的a=$\sqrt{m}$,b=2$\sqrt{2}$,c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{8+m}$,
由题意可得e=$\frac{c}{a}$=$\frac{\sqrt{8+m}}{\sqrt{m}}$=$\sqrt{5}$,
解得m=2.
故答案为:2.
点评 本题考查双曲线的方程和性质,主要是离心率,考查方程思想和运算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.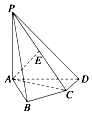 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
(1)证明:AE⊥平面PCD;
(2)求PB和平面PAD所成的角的大小.
 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.(1)证明:AE⊥平面PCD;
(2)求PB和平面PAD所成的角的大小.
15.若点P到点F(2,0)的距离比它到直线x+3=0的距离小1,则点P的轨迹方程是( )
| A. | y2=2x | B. | y2=4x | C. | y2=8x | D. | x2=8y |
10..已知O是坐标原点,点A(1,0),若点M(x,y)为平面区域$\left\{\begin{array}{l}x+y≥2\\ x≤1\\ y≤2\end{array}\right.$上的一个动点,则$|{\overrightarrow{OA}+\overrightarrow{OM}}|$的最大值是( )
| A. | $\sqrt{5}$ | B. | 1 | C. | $2\sqrt{2}$ | D. | $\frac{1}{2}$ |