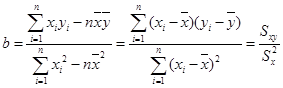题目内容
(13分)(2011•广东)在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:
| 编号n | 1 | 2 | 3 | 4 | 5 |
| 成绩xn | 70 | 76 | 72 | 70 | 72 |
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
(1)7(2)0.4
解析试题分析:(1)根据平均数公式写出这组数据的平均数表示式,在表示式中有一个未知量,根据解方程的思想得到结果,求出这组数据的方差,再进一步做出标准差.
(2)本题是一个古典概型,试验发生包含的事件是从5位同学中选2个,共有C52种结果,满足条件的事件是恰有一位成绩在区间(68,75)中,共有C41种结果,根据概率公式得到结果.
解:(1)根据平均数的个数可得75= ,
,
∴x6=90,
这六位同学的方差是 (25+1+9+25+9+225)=49,
(25+1+9+25+9+225)=49,
∴这六位同学的标准差是7
(2)由题意知本题是一个古典概型,
试验发生包含的事件是从5位同学中选2个,共有C52=10种结果,
满足条件的事件是恰有一位成绩在区间(68,75)中,共有C41=4种结果,
根据古典概型概率个数得到P= =0.4.
=0.4.
点评:本题考查一组数据的平均数公式的应用,考查求一组数据的方差和标准差,考查古典概型的概率公式的应用,是一个综合题目.

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数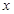 (个) (个) | 2 | 3 | 4 | 5 |
加工的时间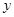 (小时) (小时) | 2.5 | 3 | 4 | 4.5 |
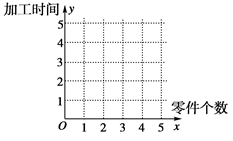
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出
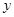 关于
关于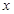 的线性回归方程
的线性回归方程 ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;(3)试预测加工
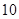 个零件需要多少时间?
个零件需要多少时间?参考公式:回归直线
 ,其中
,其中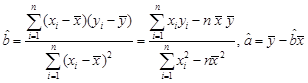 .
.
某电视台在一次对文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关数据如下表所示:
| | 文艺节目 | 新闻节目 | 总计 |
| 20岁到40岁 | 40 | 20 | 60 |
| 40岁以上 | 15 | 25 | 40 |
| 总计 | 55 | 45 | 100 |
(1)用分层抽样方法在收看新闻节目的观众中,随机抽取9名,那么40岁以上的观众应抽取几名?
(2)由表中数据分析,我们能否有99%的把握认为收看新闻节目的观众与年龄有关?(最后结果保留3位有效数字,四舍五入)
附:
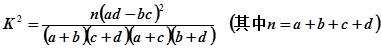
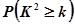 | 0.05 | 0.01 | 0.005 | 0.001 |
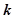 | 3.841 | 6.635 | 7.879 | 10.828 |
近年来,我国很多城市都出现了严重的雾霾天气.为了更好地保护环境,2012年国家环保部发布了新修订的《环境空气质量标准》,其中规定:居民区 的PM2.5的年平均浓度不得超过35微克/立方米.某城市环保部门在2014年1月1日到 2014年3月31日这90天对某居民区的PM2. 5平均浓度的监测数据统计如下:
| 组别 | PM2.5浓度(微克/立方米) | 频数(天) |
| 第一组 | (0,35] | 24 |
| 第二组 | (35,75] | 48 |
| 第三组 | (75,115] | 12 |
| 第四组 | >115 | 6 |
(1)在这
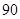 天中抽取
天中抽取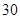 天的数据做进一步分析,每一组应抽取多少天?
天的数据做进一步分析,每一组应抽取多少天?(2)在(I)中所抽取的样本PM2. 5的平均浓度超过75(微克/立方米)的若干天中,随 机抽取2天,求至少有一天平均浓度超过115(微克/立方米)的概率.
某学校高一年学生在某次数学单元测试中,成绩在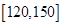 的频数分布表如下:
的频数分布表如下:
| 分数 |  | 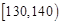 | 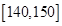 |
| 频数 | 60 | 20 | 20 |
(1)用分层抽样的方法从成绩在
 ,
,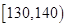 和
和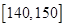 的同学中共抽取
的同学中共抽取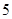 人,其中成绩在
人,其中成绩在 的有几人?
的有几人?(2)从(1)中抽出的
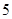 人中,任取
人中,任取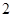 人,求成绩在
人,求成绩在 和
和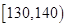 中各有
中各有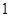 人的概率?
人的概率? 某工厂有工人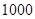 人,其中
人,其中 名工人参加过短期培训(称为
名工人参加过短期培训(称为 类工人),另外
类工人),另外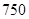 名工人参加过长期培训(称为
名工人参加过长期培训(称为 类工人).现用分层抽样的方法(按
类工人).现用分层抽样的方法(按 类、
类、 类分二层)从该工厂的工人中共抽查
类分二层)从该工厂的工人中共抽查 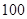 名工人,调查他们的生产能力(此处的生产能力指一天加工的零件数).
名工人,调查他们的生产能力(此处的生产能力指一天加工的零件数).
(1) 类工人和
类工人和 类工人中各抽查多少工人?
类工人中各抽查多少工人?
(2)从 类工人中的抽查结果和从
类工人中的抽查结果和从 类工人中的抽查结果分别如下表1和表2.
类工人中的抽查结果分别如下表1和表2.
表1
| 生产能力分组 | 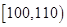 | 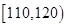 |  | 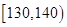 | 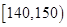 |
| 人数 | 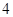 |  |  | 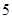 |  |
| 生产能力分组 | 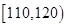 |  | 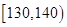 | 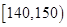 |
| 人数 |  |  |  |  |
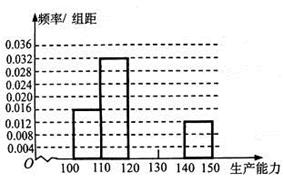
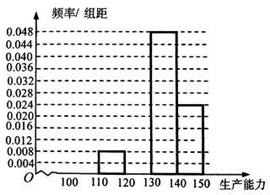
①求
 、
、 ,再完成下列频率分布直方图;
,再完成下列频率分布直方图;②分别估计
 类工人和
类工人和 类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组
类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组中的数据用该组区间的中点值作代表).
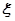 的分布列。
的分布列。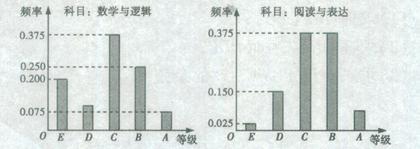
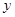 (万元)和房屋的面积
(万元)和房屋的面积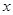 (
( )的数据 ,若由资料可知
)的数据 ,若由资料可知
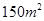 时的销售价格.
时的销售价格.