题目内容
某学校高一年学生在某次数学单元测试中,成绩在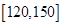 的频数分布表如下:
的频数分布表如下:
| 分数 |  | 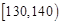 | 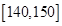 |
| 频数 | 60 | 20 | 20 |
(1)用分层抽样的方法从成绩在
 ,
,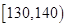 和
和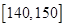 的同学中共抽取
的同学中共抽取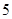 人,其中成绩在
人,其中成绩在 的有几人?
的有几人?(2)从(1)中抽出的
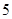 人中,任取
人中,任取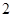 人,求成绩在
人,求成绩在 和
和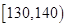 中各有
中各有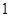 人的概率?
人的概率?
(1)3人;(2)
解析试题分析:(1)根据成绩在 、
、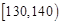 、
、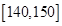 ]三组内的频数,计算出总人数然后根据分层抽样的定义即可得到结论;
]三组内的频数,计算出总人数然后根据分层抽样的定义即可得到结论;
(2)从(1)中抽出的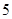 人中,成绩在
人中,成绩在 的有
的有 名同学,记为
名同学,记为 ,成绩在
,成绩在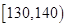 和
和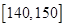 的各有1名同学,则从(1)中抽出的
的各有1名同学,则从(1)中抽出的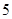 人中,列出任取
人中,列出任取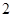 人的所有情况为10个,记事件
人的所有情况为10个,记事件 ,其包含的基本事件有
,其包含的基本事件有 个,由古典概型即可求出
个,由古典概型即可求出 .
.
(1)根据频数分布表,成绩在 ,
,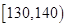 ,
,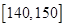 中共有
中共有 人,
人,
成绩在 的有
的有 人,故用分层抽样的方法抽取成绩在
人,故用分层抽样的方法抽取成绩在 的人数为
的人数为 .
.
(2)从(1)中抽出的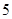 人中,成绩在
人中,成绩在 的有
的有 名同学,记为
名同学,记为 ,成绩在
,成绩在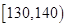 和
和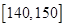 的各有1名同学,分别记为
的各有1名同学,分别记为 和
和 ,则从(1)中抽出的
,则从(1)中抽出的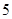 人中,列出任取
人中,列出任取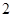 人的所有情况为
人的所有情况为 ,
,
共有 个基本事件,记事件
个基本事件,记事件 ,
,
其包含的基本事件有 个,分别是
个,分别是 ,
,
故 .
.
考点:频数分布表,分层抽样,古典概型

练习册系列答案
相关题目
(13分)(2011•广东)在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:
| 编号n | 1 | 2 | 3 | 4 | 5 |
| 成绩xn | 70 | 76 | 72 | 70 | 72 |
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
(2014·泰安模拟)某中学为研究学生的身体素质与课外体育锻炼时间的关系,对400名高一学生的一周课外体育锻炼时间进行调查,结果如下表所示:
| 锻炼时间 (分钟) | [0,20) | [20,40) | [40,60) | [60,80) | [80,100) | [100,120) |
| 人数 | 40 | 60 | 80 | 100 | 80 | 40 |
(1)其中课外体育锻炼时间在
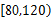 分钟内的学生应抽取多少人?
分钟内的学生应抽取多少人?(2)若从(1)中被抽取的学生中随机抽取2名,求这2名学生课外体育锻炼时间均在
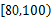 分钟内的概率.
分钟内的概率. 大家知道,莫言是中国首位获得诺贝尔奖的文学家,国人欢欣鼓舞.某高校文学社从男女生中各抽取50名同学调查对莫言作品的了解程度,结果如下:
| 阅读过莫言的 作品数(篇) | 0~25 | 26~50 | 51~75 | 76~100 | 101~130 |
| 男生 | 3 | 6 | 11 | 18 | 12 |
| 女生 | 4 | 8 | 13 | 15 | 10 |
(2)对莫言作品阅读超过75篇的则称为“对莫言作品非常了解”,否则为“一般了解”.根据题意完成下表,并判断能否有75%的把握认为对莫言作品的非常了解与性别有关?
| | 非常了解 | 一般了解 | 合计 |
| 男生 | | | |
| 女生 | | | |
| 合计 | | | |
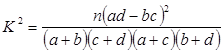
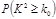 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
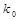 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
 与销售额
与销售额 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据: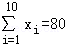 ,
, ,
, ,
,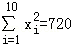 .
. ,
,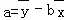 ,其中
,其中 ,
, 为样本平均值,线性回归方程也可写为
为样本平均值,线性回归方程也可写为 .
.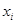 (年)与所支出的维修费
(年)与所支出的维修费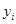 (万元)的数据资料算得如下结果,
(万元)的数据资料算得如下结果,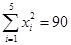 ,
,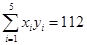 ,
,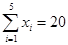 ,
,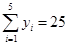 .
.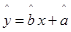 ;
;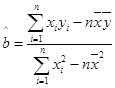 ,
,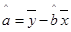 ,其中
,其中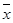 ,
, 为样本平均值.)
为样本平均值.)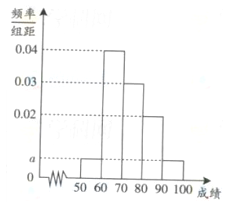




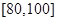 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份的分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份的分数在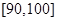 之间的概率;
之间的概率;