题目内容
5．求函数y=（$\frac{1}{3}$）${\;}^{-2{x}^{2}-8x+1}$（-3≤x≤1）的单调区间与值域．分析 根据题意，设t=-2x2-8x+1，求出t在-3≤x≤1时的值域，再求y=${（\frac{1}{3}）}^{t}$的值域；根据复合函数的单调性求出函数y=${（\frac{1}{3}）}^{-{2x}^{2}-8x+1}$的单调区间．
解答 解：∵函数y=（$\frac{1}{3}$）${\;}^{-2{x}^{2}-8x+1}$（-3≤x≤1），
设t=-2x2-8x+1，-3≤x≤1；
∴t=-2（x+2）2+9，
当-3≤x≤1时，-9≤t≤9，
∴${（\frac{1}{3}）}^{9}$≤${（\frac{1}{3}）}^{t}$≤${（\frac{1}{3}）}^{-9}$，
即3-9≤${（\frac{1}{3}）}^{t}$≤39；
∴函数y=${（\frac{1}{3}）}^{t}$在x∈[1，3]上的值域是[3-9，39]；
又原函数是由y=${（\frac{1}{3}）}^{t}$和t=-2x2-8x+1两个函数符合而成，
第一个函数是单调减函数，第二个函数在区间[-3，-2]上是单调增函数，
在区间（-2，1]上是单调减函数，
∴函数y=${（\frac{1}{3}）}^{-{2x}^{2}-8x+1}$的单调减区间是[-3，-2]，单调增区间是（-2，1]．
点评 本题考查了指数型复合函数的应用问题，求值域时要分两步，第一步求出内层函数在定义域上的值域，第二步求外层函数在内层函数值域上的值域，是综合性题目．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
目标测试系列答案
相关题目
16．
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的部分图象如图所示，当$x∈[0，\frac{π}{2}]$时，满足f（x）=1的x的值为（ ）
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的部分图象如图所示，当$x∈[0，\frac{π}{2}]$时，满足f（x）=1的x的值为（ ）| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{5π}{24}$ | D． | $\frac{π}{3}$ |
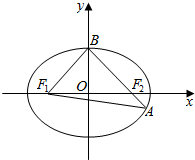如图所示，已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率e=$\frac{\sqrt{2}}{2}$，左，右焦点分别为F1，F2上顶点为B，延长BF2交椭圆C于点A，且△ABF1的周长为8．