题目内容
12.$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$是两个互相垂直的单位向量,且$\overrightarrow{a}$=-(2$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$),$\overrightarrow{b}$=$\overrightarrow{{e}_{1}}$-λ$\overrightarrow{{e}_{2}}$(1)若$\overrightarrow{a}$∥$\overrightarrow{b}$,则λ=-$\frac{1}{2}$平行时反向(填同向或反向)
(2)若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则λ=2.
分析 (1)由题意可得$\overrightarrow{a}$=(-2,-1),$\overrightarrow{b}$=(1,-λ),运用向量共线的坐标表示,解方程即可得到;
(2)运用向量垂直的条件:数量积为0,计算即可得到所求值.
解答 解:(1)由$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$是两个互相垂直的单位向量,
可设$\overrightarrow{a}$=(-2,-1),$\overrightarrow{b}$=(1,-λ),
若$\overrightarrow{a}$∥$\overrightarrow{b}$,即有-1=2λ,解得λ=-$\frac{1}{2}$;
(2)若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则-2×1+(-1)×(-λ)=0,
解得λ=2.
故答案为:-$\frac{1}{2}$,反向,-2.
点评 本题考查向量的共线和垂直的条件:数量积为0,考查运算能力,属于基础题.

练习册系列答案
相关题目
2.在ABC中,角A、B、C的对边分别为a、b、c,若$\frac{cosA}{a}+\frac{cosC}{c}=\frac{1}{b}$,则( )
| A. | a、b、c成等比数列 | B. | a、b、c成等差数列 | ||
| C. | a2、b2、c2成等比数列 | D. | a2、b2、c2成等差数列 |
17.若直线l与两直线y=1,直线x-y-7=0分别交于M,N两点且MN的中点为P(1,-1),则直线l的斜率等于( )
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
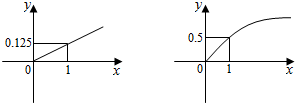 某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比,已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图).
某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比,已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图).