题目内容
若0<α<
,0<β<
,且cosα=
,tanβ=
,则α+β= .
| π |
| 2 |
| π |
| 2 |
7
| ||
| 10 |
| 4 |
| 3 |
考点:两角和与差的正切函数
专题:三角函数的求值
分析:由条件利用同角三角函数的基本关系求出tanα的值,再利用两角和的正切公式求得tan(α+β)的值,再结合α、β的范围,可得α+β的值.
解答:
解:0<α<
,0<β<
,且cosα=
,∴sinα=
,∴tanα=
=
.
又tanβ=
,tan(α+β)=
=
=
,
∴α+β=arctan
,
故答案为:arctan
.
| π |
| 2 |
| π |
| 2 |
7
| ||
| 10 |
| ||
| 10 |
| sinα |
| cosα |
| 1 |
| 7 |
又tanβ=
| 4 |
| 3 |
| tanα+tanβ |
| 1-tanα•tanβ |
| ||||
1-
|
| 31 |
| 17 |
∴α+β=arctan
| 31 |
| 17 |
故答案为:arctan
| 31 |
| 17 |
点评:本题主要考查同角三角函数的基本关系、两角和的正切公式的应用,属于基础题.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
在△ABC中已知b=2,B=
,C=
,则△ABC的面积( )
| π |
| 6 |
| π |
| 4 |
A、2
| ||
B、
| ||
C、2
| ||
D、
|
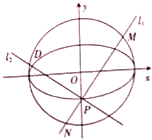 已知椭圆E:
已知椭圆E: